Tag: JComputChem
| Authors: |
Danny E. P. Vanpoucke |
| Journal: |
J. Comput. Chem. 34(5), i-ii (2013) |
| doi: |
10.1002/jcc.23239 |
| IF(2013): |
3.601 |
| export: |
bibtex |
| pdf: |
<J.Comput.Chem.> |
The image shows an isosurface of Hirshfeld-I “atoms in molecules” for Ti-doped CeO2, taken at an electron density of 0.03e/Å3, as presented by Danny E. P. Vanpoucke, Patrick Bultinck, and Isabel Van Driessche on page 405. The cubic Ce0.75Ti0.25O2 unit cell is shown along the 111 direction. The different atoms are still clearly distinguishable at this iso-surface level, and show the Ti atom in the corners to be much smaller than the Ce atoms on the sides. In this issue, this implementation of the Hirshfeld- I method for solids is published back to back with a Comment from Thomas A. Manz and the authors’ Reply.

Permanent link to this article: https://dannyvanpoucke.be/paper2013_hicover-en/
| Authors: |
Danny E. P. Vanpoucke, Isabel Van Driessche, and Patrick Bultinck |
| Journal: |
J. Comput. Chem. 34(5), 422-427 (2013) |
| doi: |
10.1002/jcc.23193 |
| IF(2013): |
3.601 |
| export: |
bibtex |
| pdf: |
<J.Comput.Chem.> <arXiv> |
 |
Graphical Abstract:The issues raised in the preceding comment are addressed. It is shown why Hirshfeld-I is, from a theoretical point of view, a good method for defining AIM and obtaining charges. Charges for a set of ionic systems are calculated using our presented method and shown to be chemically feasable. Comparison of pseudo-density to all-electron based results shows the pseudo-densities to be sufficient to obtain all-electron quality results. Timing results for systems containing hundreds of atoms. |
The issues raised in the comment by Manz are addressed through the presentation of calculated atomic charges for NaF, NaCl, MgO, SrTiO3, and La2Ce2O7, using our previously presented method for calculating Hirshfeld-I charges in solids (Vanpoucke et al., J. Comput. Chem. doi: 10.1002/jcc.23088). It is shown that the use of pseudovalence charges is sufficient to retrieve the full all-electron Hirshfeld-I charges to good accuracy. Furthermore, we present timing results of different systems, containing up to over 200 atoms, underlining the relatively low cost for large systems. A number of theoretical issues are formulated, pointing out mainly that care must be taken when deriving new atoms in molecules methods based on “expectations” for atomic charges.
Permanent link to this article: https://dannyvanpoucke.be/paper2013_hireply-en/
| Authors: |
Danny E. P. Vanpoucke, Patrick Bultinck, and Isabel Van Driessche, |
| Journal: |
J. Comput. Chem. 34(5), 405-417 (2013) |
| doi: |
10.1002/jcc.23088 |
| IF(2013): |
3.601 |
| export: |
bibtex |
| pdf: |
<J.Comput.Chem.> <arXiv> |
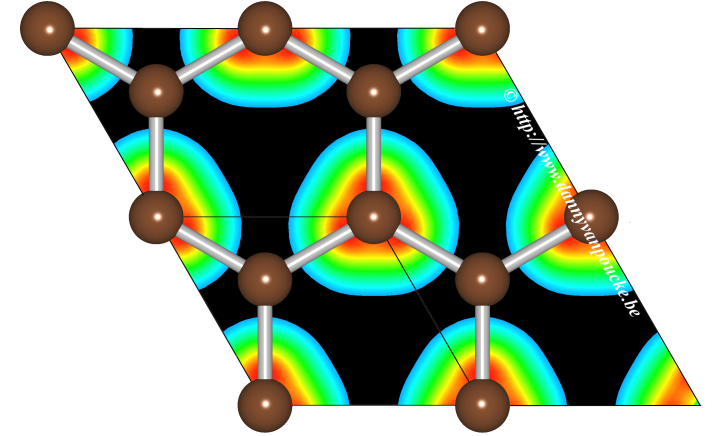 |
Graphical Abstract: The Hirshfeld-I method is extended to solids, allowing for the partitioning of a solid density into constituent atoms. The use of precalculated density grids makes the implementation code independent, and the use of pseudo-potential based electron density distributions is shown to give qualitatively the same results as all electron densities. Results for some simple solids/periodic systems like cerium oxide and graphene are presented. |
In this work, a method is described to extend the iterative Hirshfeld-I method, generally used for molecules, to periodic systems. The implementation makes use of precalculated pseudopotential-based electron density distributions, and it is shown that high-quality results are obtained for both molecules and solids, such as ceria, diamond, and graphite. The use of grids containing (precalculated) electron densities makes the implementation independent of the solid state or quantum chemical code used for studying the system. The extension described here allows for easy calculation of atomic charges and charge transfer in periodic and bulk systems. The conceptual issue of obtaining reference densities for anions is discussed, and the delocalization problem for anionic reference densities originating from the use of a plane wave basis set is identified and handled.
Permanent link to this article: https://dannyvanpoucke.be/paper2013_hipaper-en/




