Today we had our fourth consortium meeting for the DigiLignin project. Things are moving along nicely, with a clear experimental database almost done by VITO, the Machine Learning model taking shape at UMaastricht, and quantum mechanical modeling providing some first insights.
Tag: theory and experiment
Permanent link to this article: https://dannyvanpoucke.be/digilignin-c4-en/
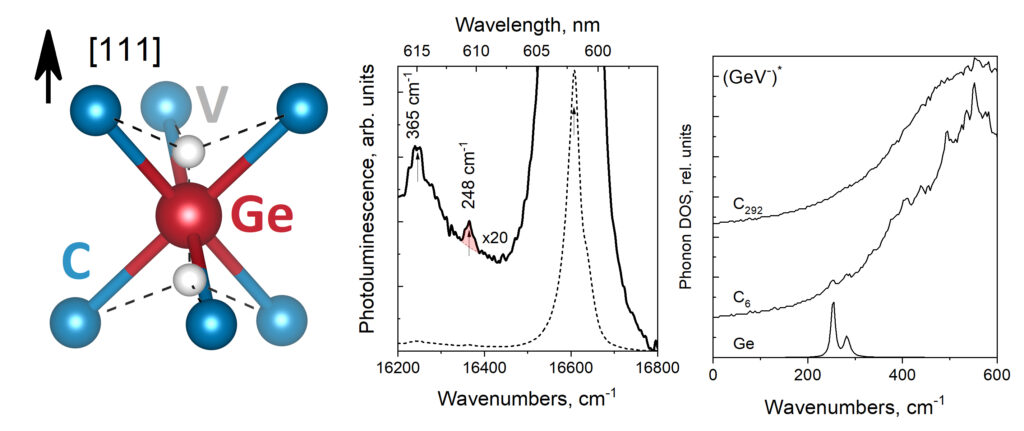
Permanent link to this article: https://dannyvanpoucke.be/paper_gevpldft_vadim-en/
Mar 10 2022
On the influence of water on THz vibrational spectral features of molecular crystals
| Authors: | Sergey Mitryukovskiy, Danny E. P. Vanpoucke, Yue Bai, Théo Hannotte, Mélanie Lavancier, Djamila Hourlier, Goedele Roos and Romain Peretti |
| Journal: | Physical Chemistry Chemical Physics 24, 6107-6125 (2022) |
| doi: | 10.1039/D1CP03261E |
| IF(2020): | 3.676 |
| export: | bibtex |
| pdf: | <PCCP> |
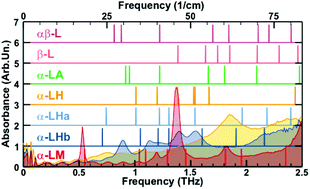 |
| Graphical Abstract: Comparison of the measured THz spectrum of 3 phases of Lactose-Monohydrate to the calculated spectra for several Lactose configurations with varying water content. |
Abstract
The nanoscale structure of molecular assemblies plays a major role in many (µ)-biological mechanisms. Molecular crystals are one of the most simple of these assemblies and are widely used in a variety of applications from pharmaceuticals and agrochemicals, to nutraceuticals and cosmetics. The collective vibrations in such molecular crystals can be probed using terahertz spectroscopy, providing unique characteristic spectral fingerprints. However, the association of the spectral features to the crystal conformation, crystal phase and its environment is a difficult task. We present a combined computational-experimental study on the incorporation of water in lactose molecular crystals, and show how simulations can be used to associate spectral features in the THz region to crystal conformations and phases. Using periodic DFT simulations of lactose molecular crystals, the role of water in the observed lactose THz spectrum is clarified, presenting both direct and indirect contributions. A specific experimental setup is built to allow the controlled heating and corresponding dehydration of the sample, providing the monitoring of the crystal phase transformation dynamics. Besides the observation that lactose phases and phase transformation appear to be more complex than previously thought – including several crystal forms in a single phase and a non-negligible water content in the so-called anhydrous phase – we draw two main conclusions from this study. Firstly, THz modes are spread over more than one molecule and require periodic computation rather than a gas-phase one. Secondly, hydration water does not only play a perturbative role but also participates in the facilitation of the THz vibrations.
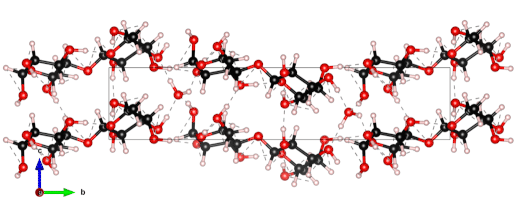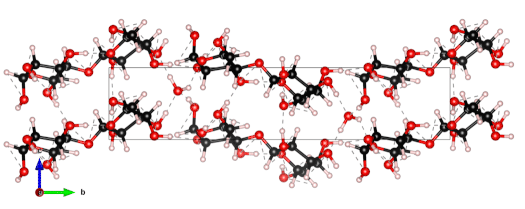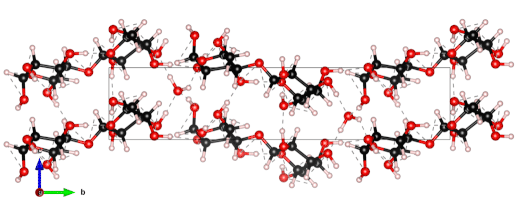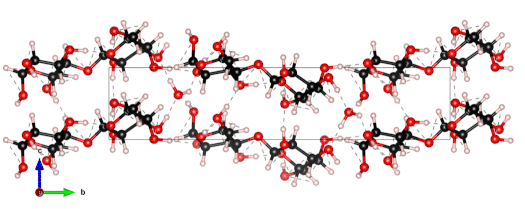
The 0.5 THz finger-print mode of alpha-lactose monohydrate.
Permanent link to this article: https://dannyvanpoucke.be/paper-lactosethz_romain-en/
Jan 21 2022
Deep Eutectic Solvents as Non-flammable Electrolytes for Durable Sodium-ion Batteries
| Authors: | Dries De Sloovere, Danny E. P. Vanpoucke, Andreas Paulus, Bjorn Joos, Lavinia Calvi, Thomas Vranken, Gunter Reekmans, Peter Adriaensens, Nicolas Eshraghi, Abdelfattah Mahmoud, Frédéric Boschini, Mohammadhosein Safari, Marlies K. Van Bael, An Hardy |
| Journal: | Advanced Energy and Sustainability Research 3(3), 2100159 (2022) |
| doi: | 10.1002/aesr.202100159 |
| IF(2022): | ?? |
| export: | bibtex |
| pdf: | <AdvEnSusRes> (OA) |
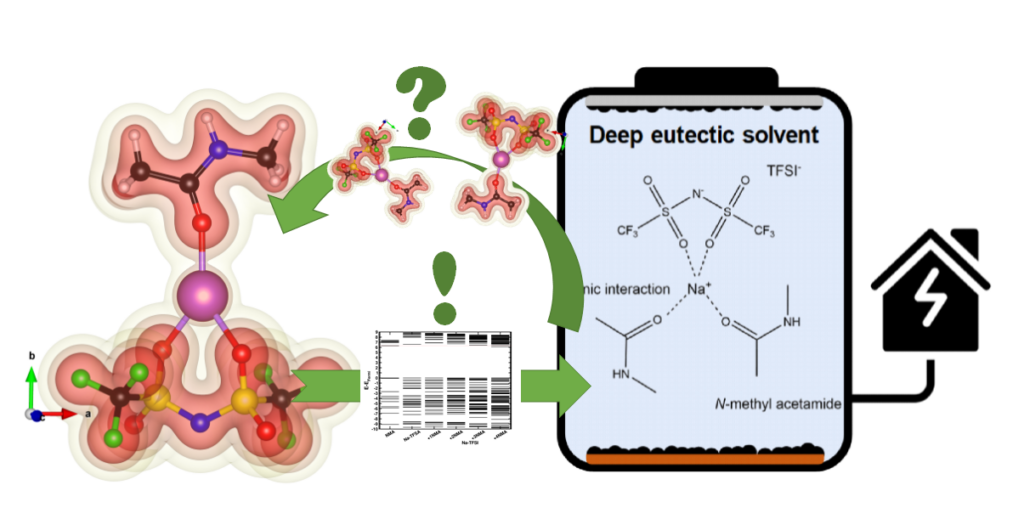 |
| Graphical Abstract: Understanding the electronic structure of Na-TFSI interacting with NMA. |
Abstract
Sodium-ion batteries are alternatives for lithium-ion batteries in applications where cost-effectiveness is of primary concern, such as stationary energy storage. The stability of sodium-ion batteries is limited by the current generation of electrolytes, particularly at higher temperatures. Therefore, the search for an electrolyte which is stable at these temperatures is of utmost importance. Here, we introduce such an electrolyte using non-flammable deep eutectic solvents, consisting of sodium bis(trifluoromethane)sulfonimide (NaTFSI) dissolved in N-methyl acetamide (NMA). Increasing the NaTFSI concentration replaces NMA-NMA hydrogen bonds with strong ionic interactions between NMA, Na+, and TFSI–. These interactions lower NMA’s HOMO energy level compared to that of TFSI–, leading to an increased anodic stability (up to ~4.65 V vs Na+/Na). (Na3V2(PO4)2F3/CNT)/(Na2+xTi4O9/C) full cells show 74.8% capacity retention after 1000 cycles at 1 C and 55 °C, and 97.0% capacity retention after 250 cycles at 0.2 C and 55 °C. This is considerably higher than for (Na3V2(PO4)2F3/CNT)/(Na2+xTi4O9/C) full cells containing a conventional electrolyte. According to the electrochemical impedance analysis, the improved electrochemical stability is linked to the formation of more robust surface films at the electrode/electrolyte interface. The improved durability and safety highlight that deep eutectic solvents can be viable electrolyte alternatives for sodium-ion batteries.
Permanent link to this article: https://dannyvanpoucke.be/paper-desbatteries_dries-en/
Oct 22 2020
Impact of methane concentration on surface morphology and boron incorporation of heavily boron-doped single crystal diamond layers
| Authors: | Rozita Rouzbahani, Shannon S.Nicley, Danny E.P.Vanpoucke, Fernando Lloret, Paulius Pobedinskas, Daniel Araujo, Ken Haenen |
| Journal: | Carbon 172, 463-473 (2021) |
| doi: | 10.1016/j.carbon.2020.10.061 |
| IF(2019): | 8.821 |
| export: | bibtex |
| pdf: | <Carbon> |
 |
| Graphical Abstract: Artist impression of B incorporation during CVD growth of diamond. |
Abstract
The methane concentration dependence of the plasma gas phase on surface morphology and boron incorporation in single crystal, boron-doped diamond deposition is experimentally and computationally investigated. Starting at 1%, an increase of the methane concentration results in an observable increase of the B-doping level up to 1.7×1021 cm−3, while the hole Hall carrier mobility decreases to 0.7±0.2 cm2 V−1 s−1. For B-doped SCD films grown at 1%, 2%, and 3% [CH4]/[H2], the electrical conductivity and mobility show no temperature-dependent behavior due to the metallic-like conduction mechanism occurring beyond the Mott transition. First principles calculations are used to investigate the origin of the increased boron incorporation. While the increased formation of growth centers directly related to the methane concentration does not significantly change the adsorption energy of boron at nearby sites, they dramatically increase the formation of missing H defects acting as preferential boron incorporation sites, indirectly increasing the boron incorporation. This not only indicates that the optimized methane concentration possesses a large potential for controlling the boron concentration levels in the diamond, but also enables optimization of the growth morphology. The calculations provide a route to understand impurity incorporation in diamond on a general level, of great importance for color center formation.
Permanent link to this article: https://dannyvanpoucke.be/paper_bdoping-en/
Feb 25 2020
UV-Curable Biobased Polyacrylates Based on a Multifunctional 2 Monomer Derived from Furfural
| Authors: | Jules Stouten, Danny E. P. Vanpoucke, Guy Van Assche, and Katrien V. Bernaerts |
| Journal: | Macromolecules 53(4), 1388-1404 (2020) |
| doi: | 10.1021/acs.macromol.9b02659 |
| IF(2019): | 5.918 |
| export: | bibtex |
| pdf: | <Macromolecules> (Open Access) |
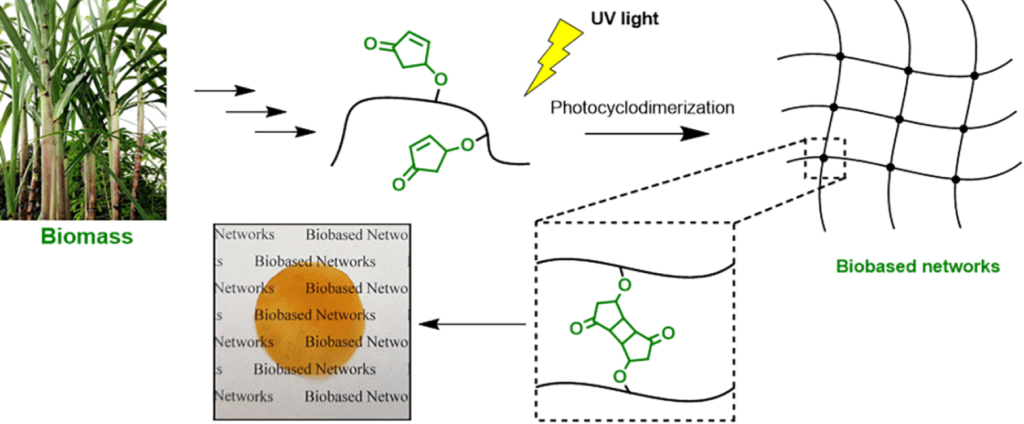 |
| Graphical Abstract: The formation of biobased polyacrylates. |
Abstract
The controlled polymerization of a new biobased monomer, 4-oxocyclopent-2-en-1-yl acrylate (4CPA), was
established via reversible addition−fragmentation chain transfer (RAFT) (co)polymerization to yield polymers bearing pendent cyclopentenone units. 4CPA contains two reactive functionalities, namely, a vinyl group and an internal double bond, and is an unsymmetrical monomer. Therefore, competition between the internal double bond and the vinyl group eventually leads to gel formation. With RAFT polymerization, when aiming for a degree of polymerization (DP) of 100, maximum 4CPA conversions of the vinyl group between 19.0 and 45.2% were obtained without gel formation or extensive broadening of the dispersity. When the same conditions were applied in the copolymerization of 4CPA with lauryl acrylate (LA), methyl acrylate (MA), and isobornyl acrylate, 4CPA conversions of the vinyl group between 63 and 95% were reached. The additional functionality of 4CPA in copolymers was demonstrated by model studies with 4-oxocyclopent-2-en-1-yl acetate (1), which readily dimerized under UV light via [2 + 2] photocyclodimerization. First-principles quantum mechanical simulations supported the experimental observations made in NMR. Based on the calculated energetics and chemical shifts, a mixture of head-to-head and head-to-tail dimers of (1) were identified. Using the dimerization mechanism, solvent-cast LA and MA copolymers containing 30 mol % 4CPA were cross-linked under UV light to obtain thin films. The cross-linked films were characterized by dynamic scanning calorimetry, dynamic mechanical analysis, IR, and swelling experiments. This is the first case where 4CPA is described as a monomer for functional biobased polymers that can undergo additional UV curing via photodimerization.
Permanent link to this article: https://dannyvanpoucke.be/paper_nmrjules-en/
Feb 18 2020
Influence of diamond crystal orientation on the interaction with biological matter
| Authors: | Viraj Damle, Kaiqi Wu, Oreste De Luca, Natalia Ortí-Casañ, Neda Norouzi, Aryan Morita, Joop de Vries, Hans Kaper, Inge Zuhorn, Ulrich Eisel, Danny E.P. Vanpoucke, Petra Rudolf, and Romana Schirhagl, |
| Journal: | Carbon 162, 1-12 (2020) |
| doi: | 10.1016/j.carbon.2020.01.115 |
| IF(2019): | 8.821 |
| export: | bibtex |
| pdf: | <Carbon> (Open Access) |
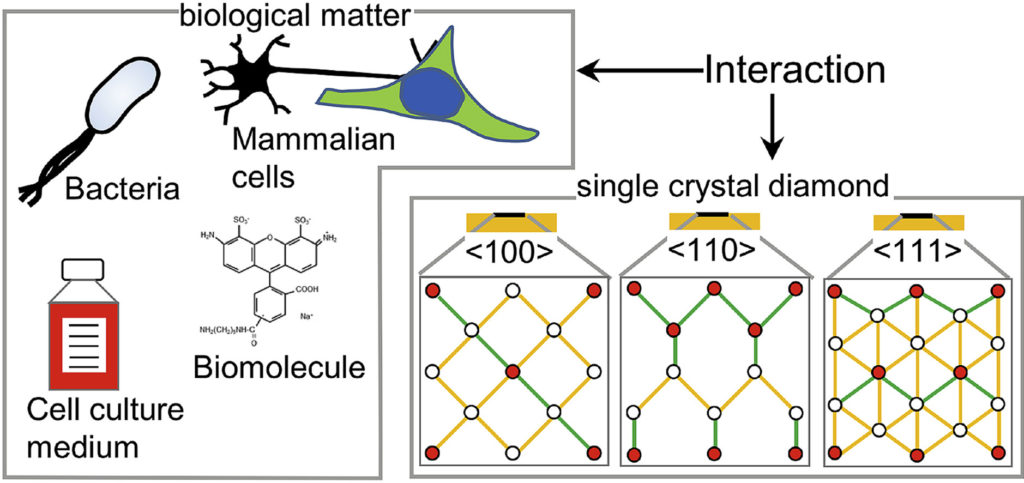 |
| Graphical Abstract: The preferential adsorption of biological matter on oriented diamond surfaces. |
Abstract
Diamond has been a popular material for a variety of biological applications due to its favorable chemical, optical, mechanical and biocompatible properties. While the lattice orientation of crystalline material is known to alter the interaction between solids and biological materials, the effect of diamond’s crystal orientation on biological applications is completely unknown. Here, we experimentally evaluate the influence of the crystal orientation by investigating the interaction between the <100>, <110> and <111> surfaces of the single crystal diamond with biomolecules, cell culture medium, mammalian cells and bacteria. We show that the crystal orientation significantly alters these biological interactions. Most surprising is the two orders of magnitude difference in the number of bacteria adhering on <111> surface compared to <100> surface when both the surfaces were maintained under the same condition. We also observe differences in how small biomolecules attach to the surfaces. Neurons or HeLa cells on the other hand do not have clear preferences for either of the surfaces. To explain the observed differences, we theoretically estimated the surface charge for these three low index diamond surfaces and followed by the surface composition analysis using x-ray photoelectron spectroscopy (XPS). We conclude that the differences in negative surface charge, atomic composition and functional groups of the different surface orientations lead to significant variations in how the single crystal diamond surface interacts with the studied biological entities.
Permanent link to this article: https://dannyvanpoucke.be/paper_diamondromanaorientation2020-en/
Permanent link to this article: https://dannyvanpoucke.be/paper_eudopingdrmspecial2018-en/
Permanent link to this article: https://dannyvanpoucke.be/paper_epsilonfenc-en/
Oct 31 2018
Daylight saving and solar time
For many people around the world, last weekend was highlighted by a half-yearly recurring ritual: switching to/from daylight saving time. In Belgium, this goes hand-in-hand with another half-yearly ritual; The discussion about the possible benefits of abolishing of daylight saving time. Throughout the last century, daylight saving time has been introduced on several occasions. The most recent introduction in Belgium and the Netherlands was in 1977. At that time it was intended as a measure for conserving energy, due to the oil-crises of the 70’s. (In Belgium, this makes it painfully modern due to the current state of our energy supplies: the impending doom of energy shortages and the accompanying disconnection plans which will put entire regions without power in case of shortages.)
The basic idea behind daylight saving time is to align the daylight hours with our working hours. A vision quite different from that of for example ancient Rome, where the daily routine was adjusted to the time between sunrise and sunset. This period was by definition set to be 12 hours, making 1h in summer significantly longer than 1h in winter. As children of our time, with our modern vision on time, it is very hard to imagine living like this without being overwhelmed by images of of impending doom and absolute chaos. In this day and age, we want to know exactly, to the second, how much time we are spending on everything (which seems to be social media mostly 😉 ). But also for more important aspects of life, a more accurate picture of time is needed. Think for example of your GPS, which will put you of your mark by hundreds of meters if your uncertainty in time is a mere 0.000001 seconds. Also, police radar will not be able to measure the speed of your car with the same uncertainty on its timing.
Turing back to the Roman vision of time, have you ever wondered why “the day” is longer during summer than during winter? Or, if this difference is the same everywhere on earth? Or, if the variation in day length is the same during the entire year?
Our place on earth
To answer these questions, we need a good model of the world around us. And as is usual in science, the more accurate the model, the more detailed the answer.
Let us start very simple. We know the earth is spherical, and revolves around it’s axis in 24h. The side receiving sunlight we call day, while the shaded side is called night. If we assume the earth rotates at a constant speed, then any point on its surface will move around the earths rotational axis at a constant angular speed. This point will spend 50% of its time at the light side, and 50% at the dark side. Here we have also silently assumed, the rotational axis of the earth is “straight up” with regard to the sun.
 In reality, this is actually not the case. The earths rotational axis is tilted by about 23° from an axis perpendicular to the orbital plane. If we now consider a fixed point on the earths surface, we’ll note that such a point at the equator still spends 50% of its time in the light, and 50% of its time in the dark. In contrast, a point on the northern hemisphere will spend less than 50% of its time on the daylight side, while a point on the southern hemisphere spends more than 50% of its time on the daylight side. You also note that the latitude plays an important role. The more you go north, the smaller the daylight section of the latitude circle becomes, until it vanishes at the polar circle. On the other hand, on the southern hemisphere, if you move below the polar circle, the point spend all its time at the daylight side. So if the earths axis was fixed with regard to the sun, as shown in the picture, we would have a region on earth living an eternal night (north pole) or day (south pole). Luckily this is not the case. If we look at the evolution of the earths axis, we see that it is “fixed with regard to the fixed stars”, but makes a full circle during one orbit around the sun.* When the earth axis points away from the sun, it is winter on the northern hemisphere, while during summer it points towards the sun. In between, during the equinox, the earth axis points parallel to the sun, and day and night have exactly the same length: 12h.
In reality, this is actually not the case. The earths rotational axis is tilted by about 23° from an axis perpendicular to the orbital plane. If we now consider a fixed point on the earths surface, we’ll note that such a point at the equator still spends 50% of its time in the light, and 50% of its time in the dark. In contrast, a point on the northern hemisphere will spend less than 50% of its time on the daylight side, while a point on the southern hemisphere spends more than 50% of its time on the daylight side. You also note that the latitude plays an important role. The more you go north, the smaller the daylight section of the latitude circle becomes, until it vanishes at the polar circle. On the other hand, on the southern hemisphere, if you move below the polar circle, the point spend all its time at the daylight side. So if the earths axis was fixed with regard to the sun, as shown in the picture, we would have a region on earth living an eternal night (north pole) or day (south pole). Luckily this is not the case. If we look at the evolution of the earths axis, we see that it is “fixed with regard to the fixed stars”, but makes a full circle during one orbit around the sun.* When the earth axis points away from the sun, it is winter on the northern hemisphere, while during summer it points towards the sun. In between, during the equinox, the earth axis points parallel to the sun, and day and night have exactly the same length: 12h.
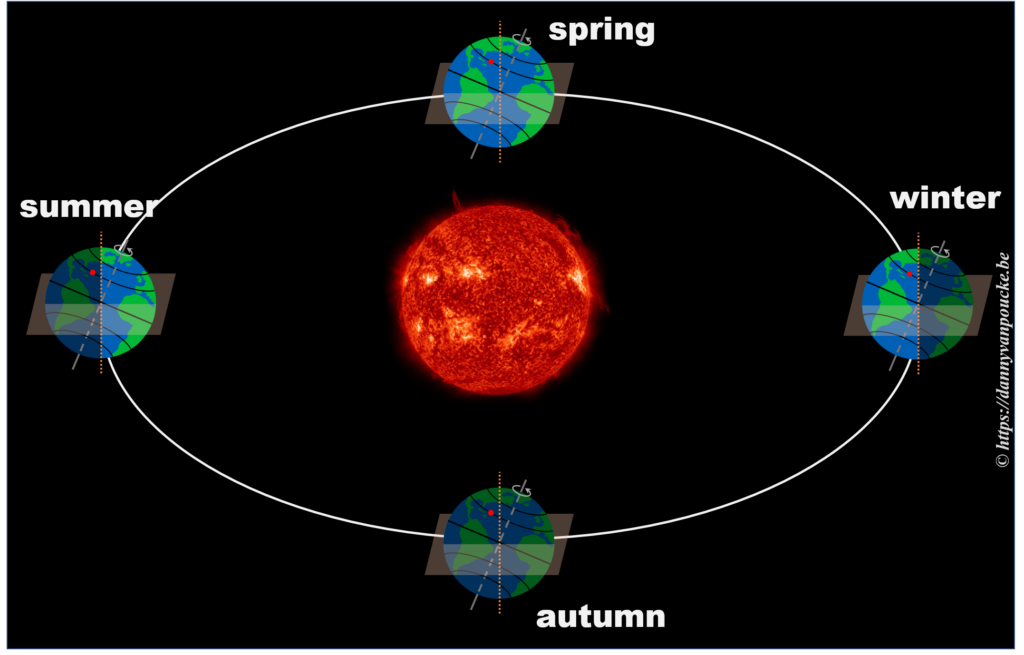
So, now that we know the length of our daytime varies with the latitude and the time of the year, we can move one step further.
How does the length of a day vary, during the year?
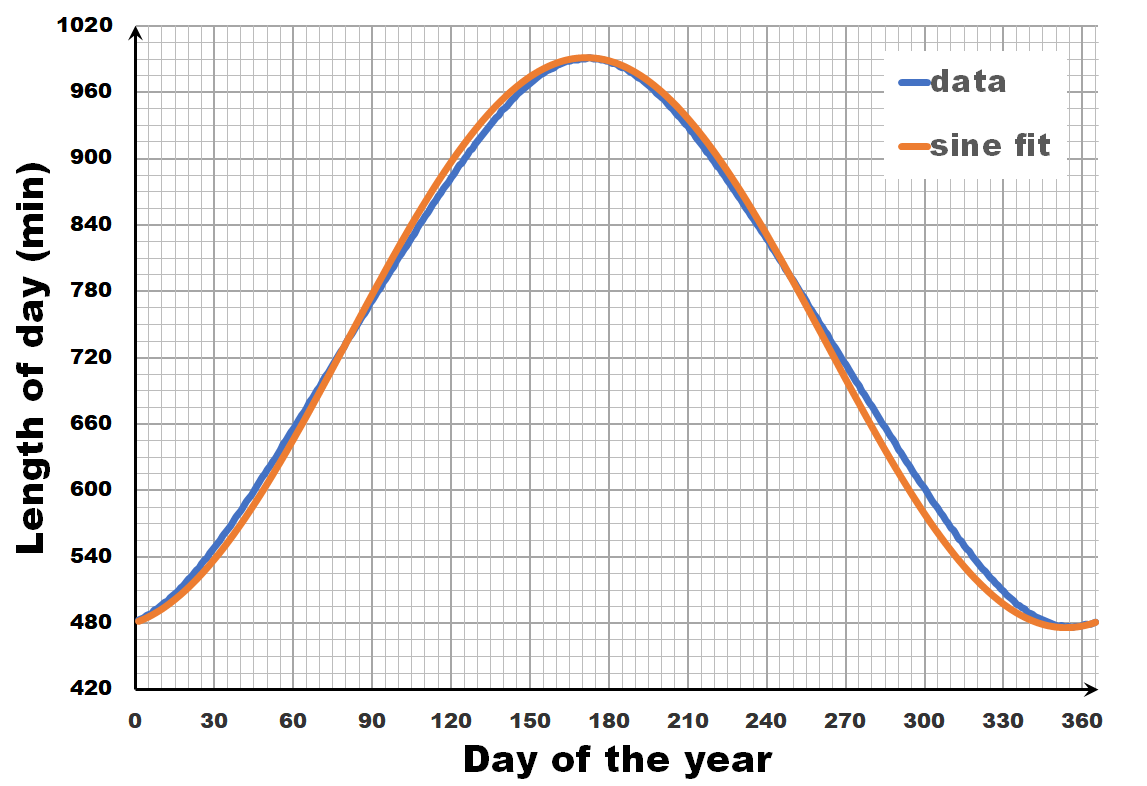
The length of the day varies over the year, with the longest and shortest days indicated by the summer and winter solstice. The periodic nature of this variation may give you the inclination to consider it as a sine wave, a sine-in-the-wild so to speak. Now let us compare a sine wave fitted to actual day-time data for Brussels. As you can see, the fit is performing quite well, but there is a clear discrepancy. So we can, and should do better than this.
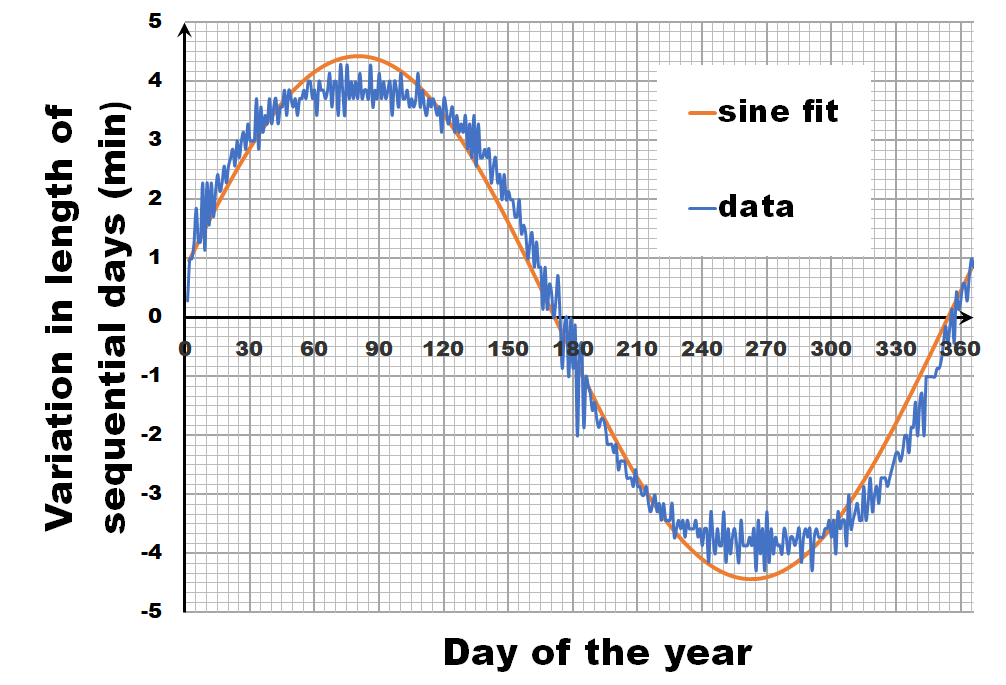
 Instead of looking at the length of each day, let us have a look at the difference in length between sequential days.** If we calculate this difference for the fitted sine wave, we again get a sine wave as we are taking a finite difference version of the derivative. In contrast, the actual data shows not a sine wave, but a broadened sine wave with flat maximum and minimum. You may think this is an error, or an artifact of our averaging, but in reality, this trend even depends on the latitude, becoming more extreme the closer you get to the poles.
Instead of looking at the length of each day, let us have a look at the difference in length between sequential days.** If we calculate this difference for the fitted sine wave, we again get a sine wave as we are taking a finite difference version of the derivative. In contrast, the actual data shows not a sine wave, but a broadened sine wave with flat maximum and minimum. You may think this is an error, or an artifact of our averaging, but in reality, this trend even depends on the latitude, becoming more extreme the closer you get to the poles.
 This additional information, provides us with the extra hint that in addition to the axial tilt of the earth axis, we also need to consider the latitude of our position. What we need to calculate is the fraction of our latitude circle (e.g. for Brussels this is 50.85°) that is illuminated by the sun, each day of the year. With some perseverance and our high school trigonometric equations, we can derive an analytic solution, which can then be calculated by, for example, excel.
This additional information, provides us with the extra hint that in addition to the axial tilt of the earth axis, we also need to consider the latitude of our position. What we need to calculate is the fraction of our latitude circle (e.g. for Brussels this is 50.85°) that is illuminated by the sun, each day of the year. With some perseverance and our high school trigonometric equations, we can derive an analytic solution, which can then be calculated by, for example, excel.
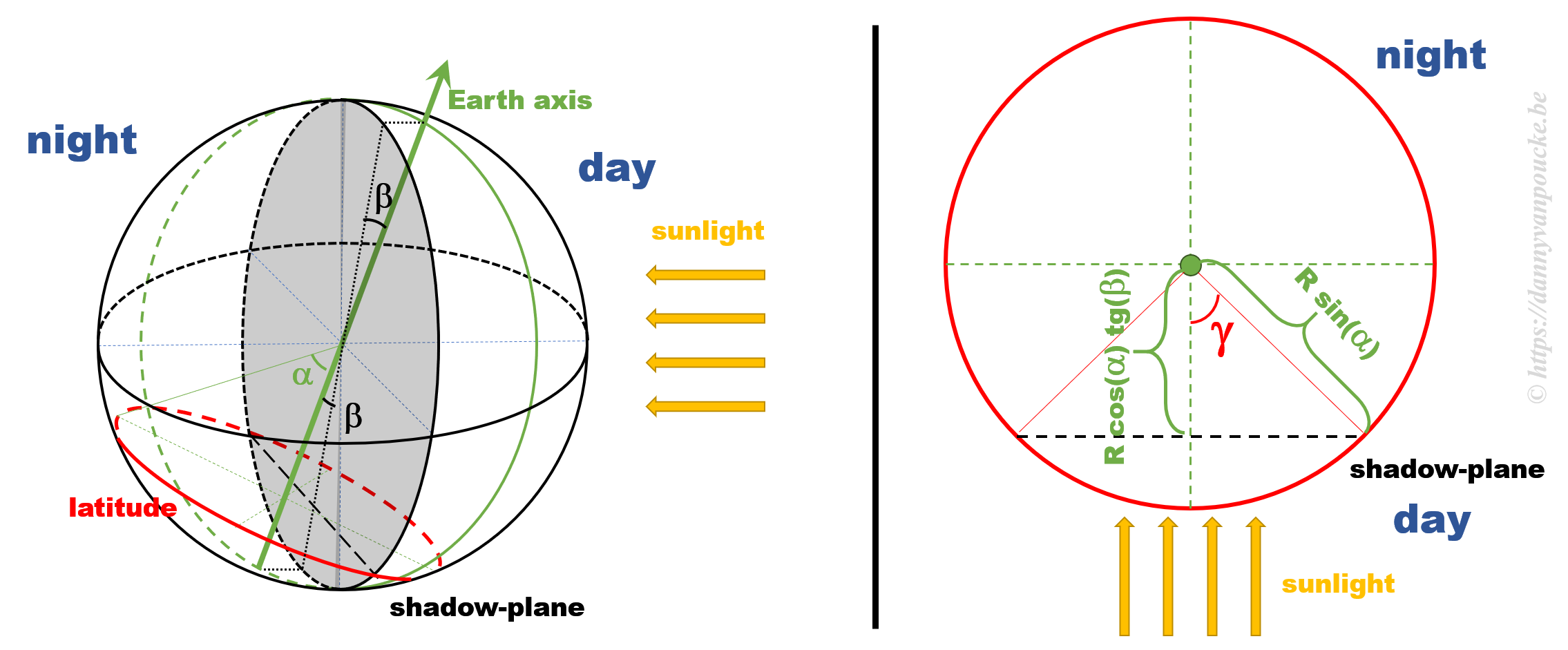 Some calculations
Some calculations
The figure above shows a 3D sketch of the situation on the left, and a 2D representation of the latitude circle on the right. α is related to the latitude, and β is the angle between the earth axis and the ‘shadow-plane’ (the plane between the day and night sides of earth). As such, β will be maximal during solstice (±23°26’12.6″) and exactly equal to zero at the equinox—when the earth axis lies entirely in the shadow-plane. This way, the length of the day is equal to the illuminated fraction of the latitude circle: 24h(360°-2γ). γ can be calculated as cos(γ)=adjacent side/hypotenuse in the right hand side part of the figure above. If we indicate the earth radius as R, then the hypotenuse is given by Rsin(α). The adjacent side, on the other hand, is found to be equal to R’sin(β), where R’=B/cos(β), and B is the perpendicular distance between the center of the earth and the plane of the latitude circle, or B=Rcos(α).
Combining all these results, we find that the number of daylight hours is:
24h*{360°-2arccos[cotg(α)tg(β)]}
How accurate is this model?
All our work is done, the actual calculation with numbers is a computer’s job, so we put excel to work. For Brussels we see that our model curve very nicely and smoothly follows the data (There is no fitting performed beyond setting the phase of the model curve to align with the data). We see that the broadening is perfectly shown, as well as the perfect estimate of the maximum and minimum variation in daytime (note that this is not a fitting parameter, in contrast to the fit with the sine wave). If you want to play with this model yourself, you can download the excel sheet here. While we are on it, I also drew some curves for different latitudes. Note that beyond the polar circles this model can not work, as we enter regions with periods of eternal day/night.

After all these calculations, be honest:
You are happy you only need to change the clock twice a year, don’t you. 🙂
* OK, in reality the earths axis isn’t really fixed, it shows a small periodic precession with a period of about 41000 years. For the sake of argument we will ignore this.
** Unfortunately, the data available for sunrises and sunsets has only an accuracy of 1 minute. By taking averages over a period of 7 years, we are able to reduce the noise from ±1 minute to a more reasonable value, allowing us to get a better picture of the general trend.
External links
- source of the daylight data: http://www.astro.oma.be/GENERAL/INFO/nzon/zon_2018.html
- I build this model about half a year ago as a response to a tweet of Philippe Smet, and the discussion with my wife Sylvia Wenmackers, who collected the daylight data, and transformed it into something easily usable.
- A Dutch version of this post can be found here
Permanent link to this article: https://dannyvanpoucke.be/daylight-saving-and-solar-time-en/
- 1
- 2