Today we had our fourth consortium meeting for the DigiLignin project. Things are moving along nicely, with a clear experimental database almost done by VITO, the Machine Learning model taking shape at UMaastricht, and quantum mechanical modeling providing some first insights.
Tag: machine learning
Permanent link to this article: https://dannyvanpoucke.be/digilignin-c4-en/
Jul 18 2022
Cover image Polymer International: A machine learning approach for the design of hyperbranched polymeric dispersing agents based on aliphatic polyesters for radiation curable inks
| Authors: | Danny E.P. Vanpoucke, Marie A.F. Delgove, Jules Stouten, Jurrie Noordijk, Nils De Vos, Kamiel Matthysen, Geert G.P. Deroover, Siamak Mehrkanoon, and Katrien V. Bernaerts |
| Journal: | Polymer International 71(8), i-i (2022) |
| doi: | 10.1002/pi.6434 |
| IF(2015): | 3.213 |
| export: | bibtex |
| pdf: | <PolymerInt> |
Abstract
The cover image is based on the Research Article A machine learning approach for the design of hyperbranched polymeric dispersing agents based on aliphatic polyesters for radiation-curable inks by Danny E.P. Vanpoucke et al., https://doi.org/10.1002/pi.6378. (The related paper can be found here.)

Cover Polymer International: Machine learning on small data sets, application on UV curable inks.
Permanent link to this article: https://dannyvanpoucke.be/paper2022_mldannycover-en/
Jul 16 2022
A machine learning approach for the design of hyperbranched polymeric dispersing agents based on aliphatic polyesters for radiation curable inks
| Authors: | Danny E.P. Vanpoucke, Marie A.F. Delgove, Jules Stouten, Jurrie Noordijk, Nils De Vos, Kamiel Matthysen, Geert G.P. Deroover, Siamak Mehrkanoon, and Katrien V. Bernaerts |
| Journal: | Polymer International 71(8), 966-975 (2022) |
| doi: | 10.1002/pi.6378 |
| IF(2021): | 3.213 |
| export: | bibtex |
| pdf: | <PI> (Open Access) (Cover Paper) |
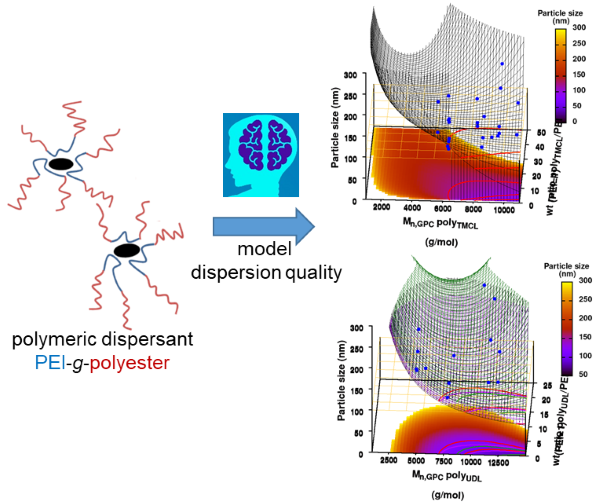 |
| Graphical Abstract:An ensemble based machine learning model for small datasets was used to predict the relationship between the dispersant structure and the pigment dispersion quality (particle size) for radiation curable formulations. |
Abstract
Polymeric dispersing agents were prepared from aliphatic polyesters consisting of δ-undecalactone (UDL) and β,δ-trimethyl-ε-caprolactones (TMCL) as biobased monomers, which are polymerized in bulk via organocatalysts. Graft copolymers were obtained by coupling of the polyesters to poly(ethylene imine) (PEI) in the bulk without using solvents. Different parameters that influence the performance of the dispersing agents in pigment based UV-curable matrices were investigated: chemistry of the polyester (UDL or TMCL), weight ratio of polyester/PEI, molecular weight of the polyesters and of PEI. The performance of the dispersing agents was modelled using machine learning in order to increase the efficiency of the dispersant design. The resulting models were presented as analytical models for the individual polyesters and the synthesis conditions for optimal performing dispersing agents were indicated as a preference for high molecular weight polyesters and a polyester dependent maximum weight ratio polyester/PEI.
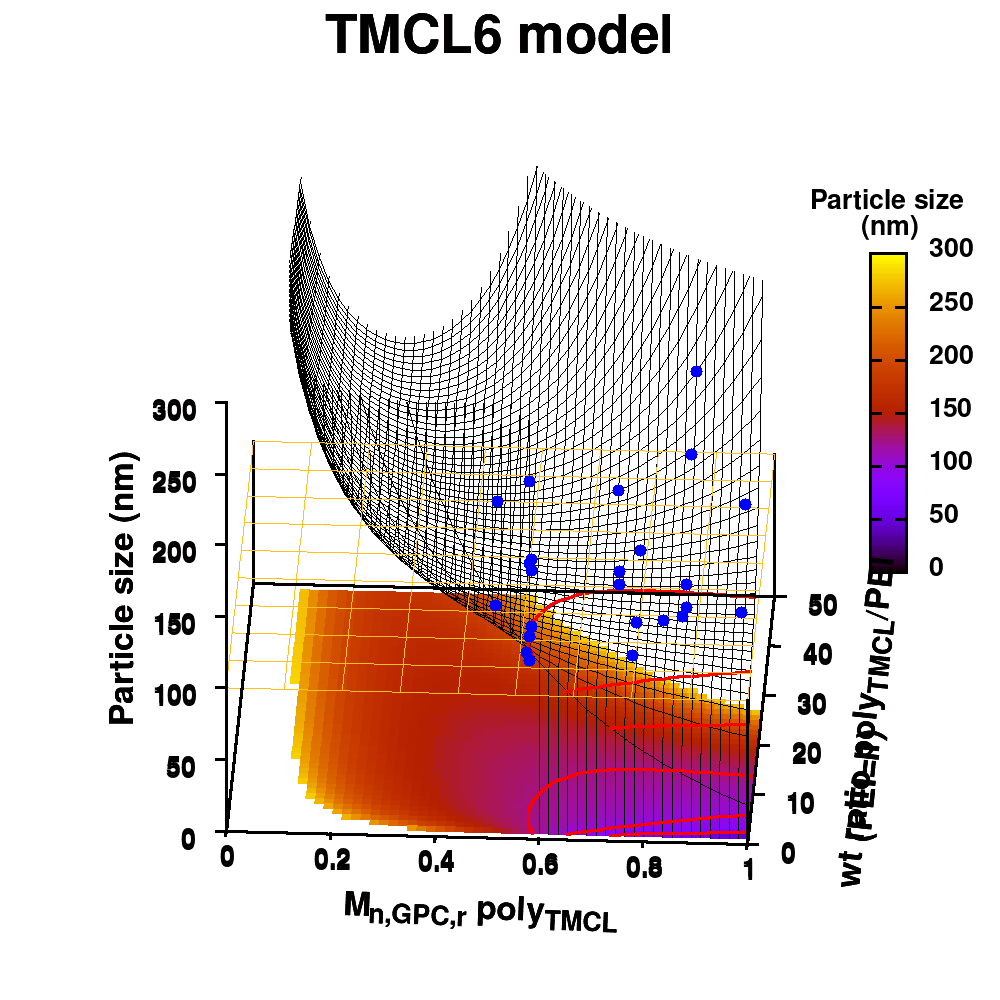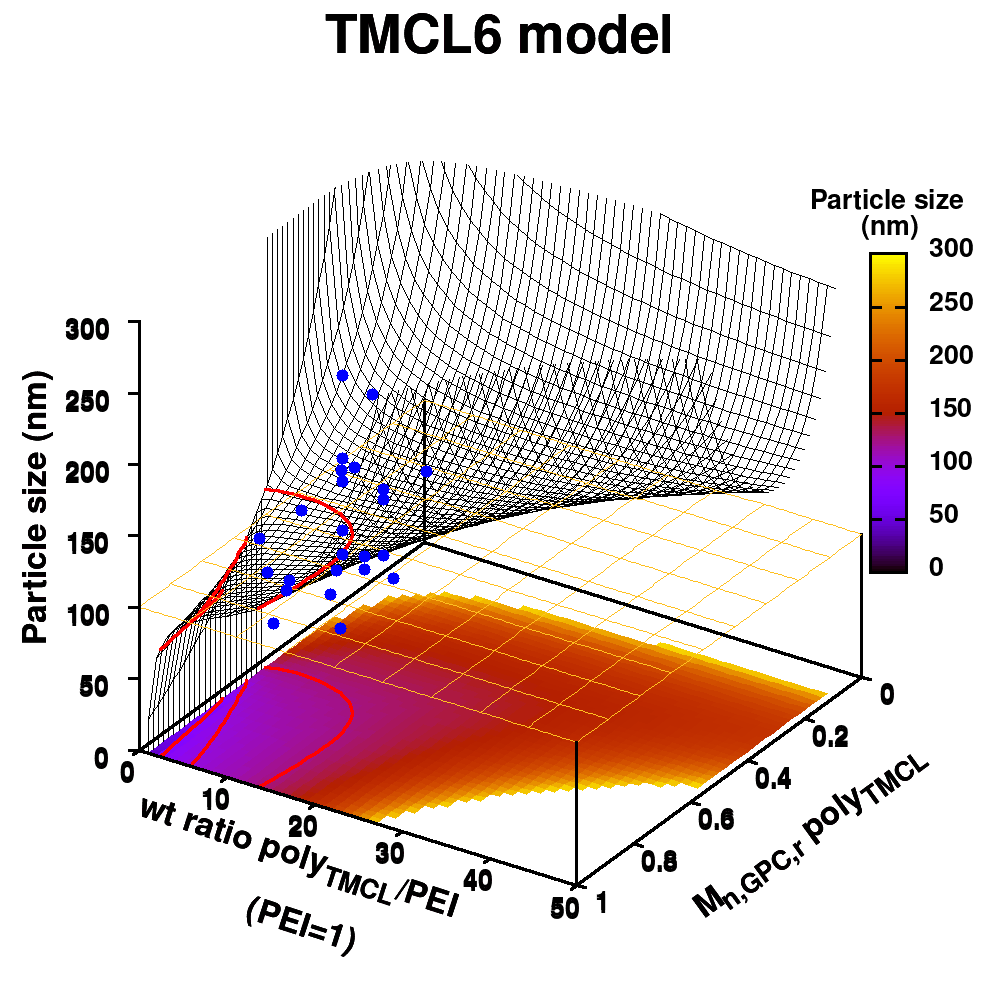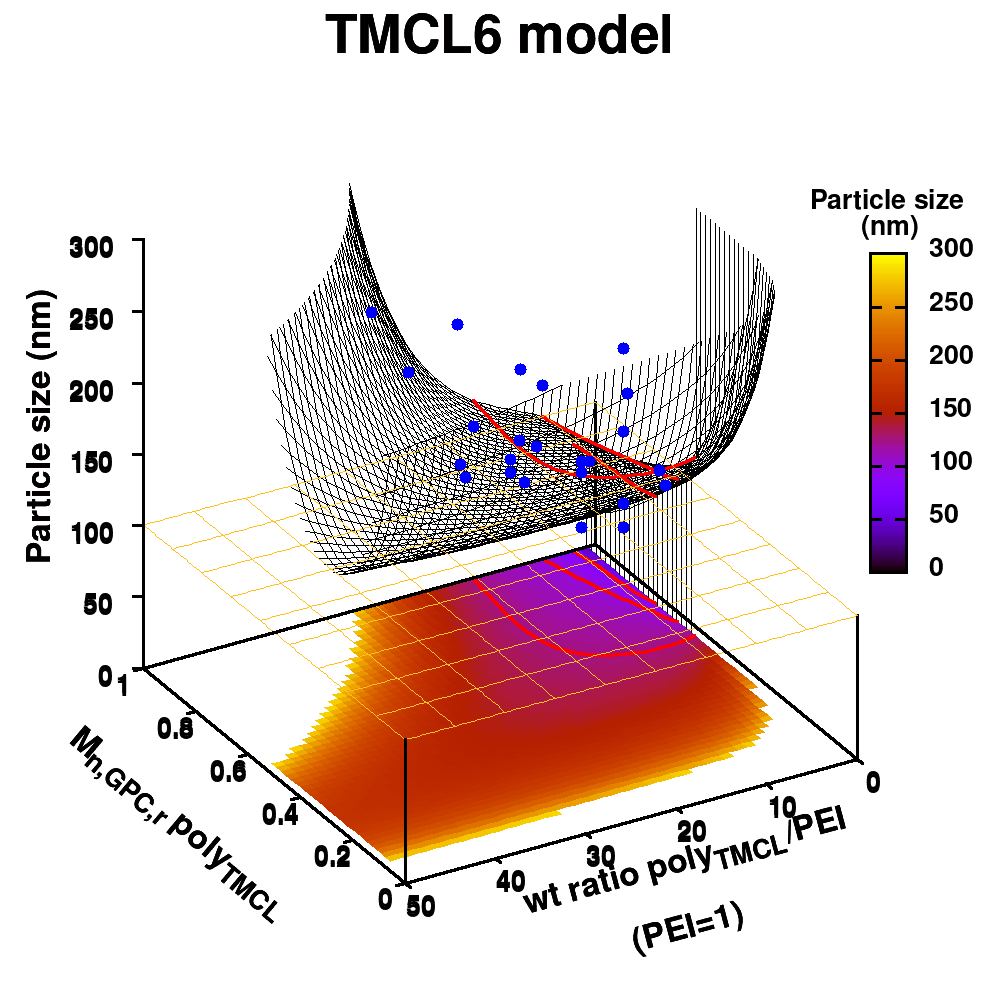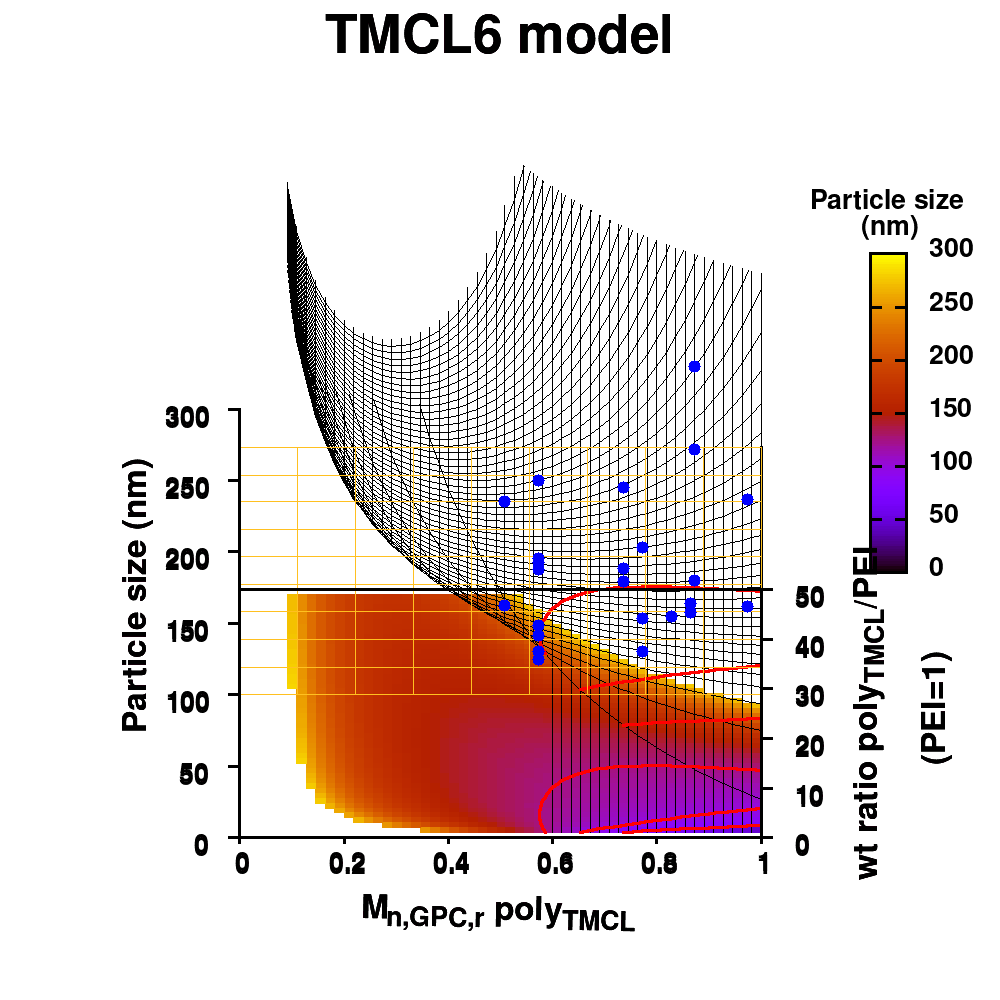
Animation of TMCL model 6
Permanent link to this article: https://dannyvanpoucke.be/paper-ml_inks_um-en/
May 06 2021
TEDx Talk: The Virtual Lab
Happy to announce my TEDxUHasselt talk is officially part of the TEDx universe: https://www.ted.com/talks/danny_vanpoucke_the_virtual_lab .
I enjoyed talking about the VirtualLab. Showed examples from atoms to galaxies, from computer-chips to drug-design and from to opinion-dynamics to epidemiology. I looked at the past and and glanced towards the future, where machine learning and artificial intelligence are the new kids on the block.
Permanent link to this article: https://dannyvanpoucke.be/tedx-talk-the-virtual-lab/
Dec 18 2020
Gnuplot animated gifs: Visualizing Machine-Learning models
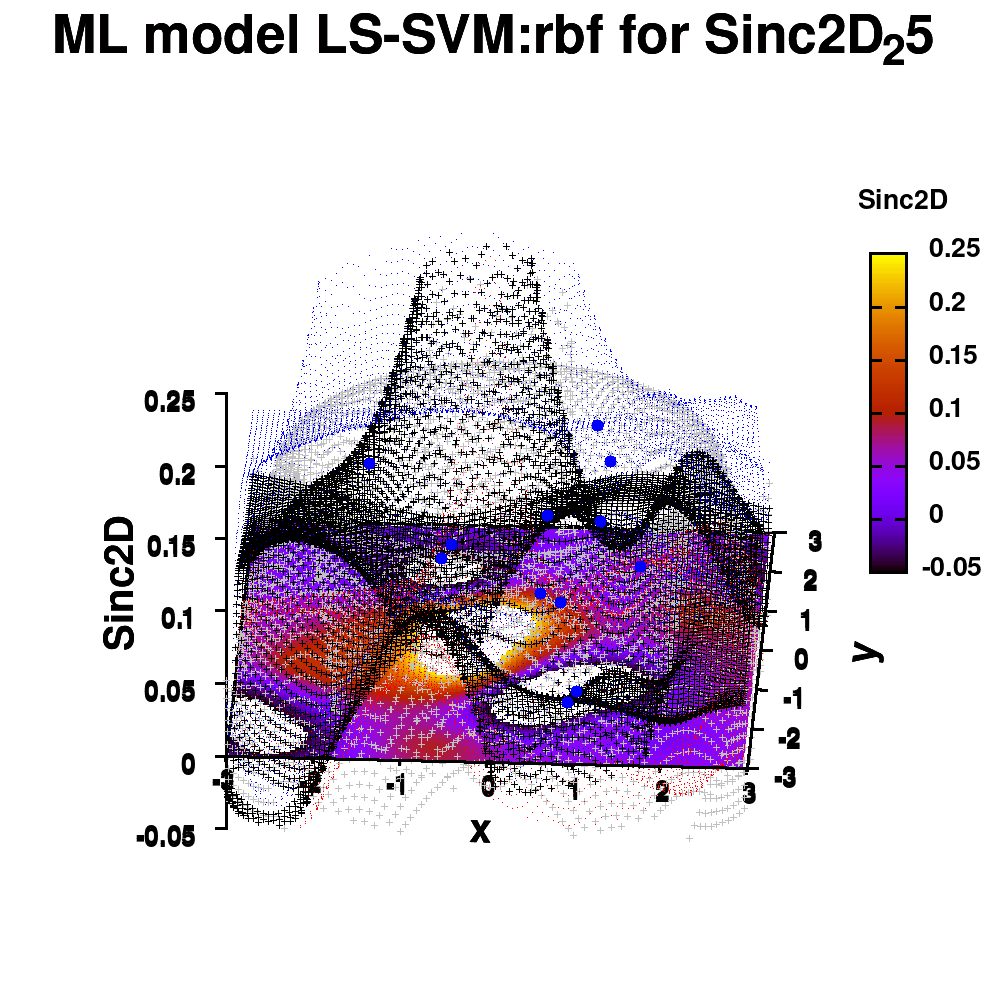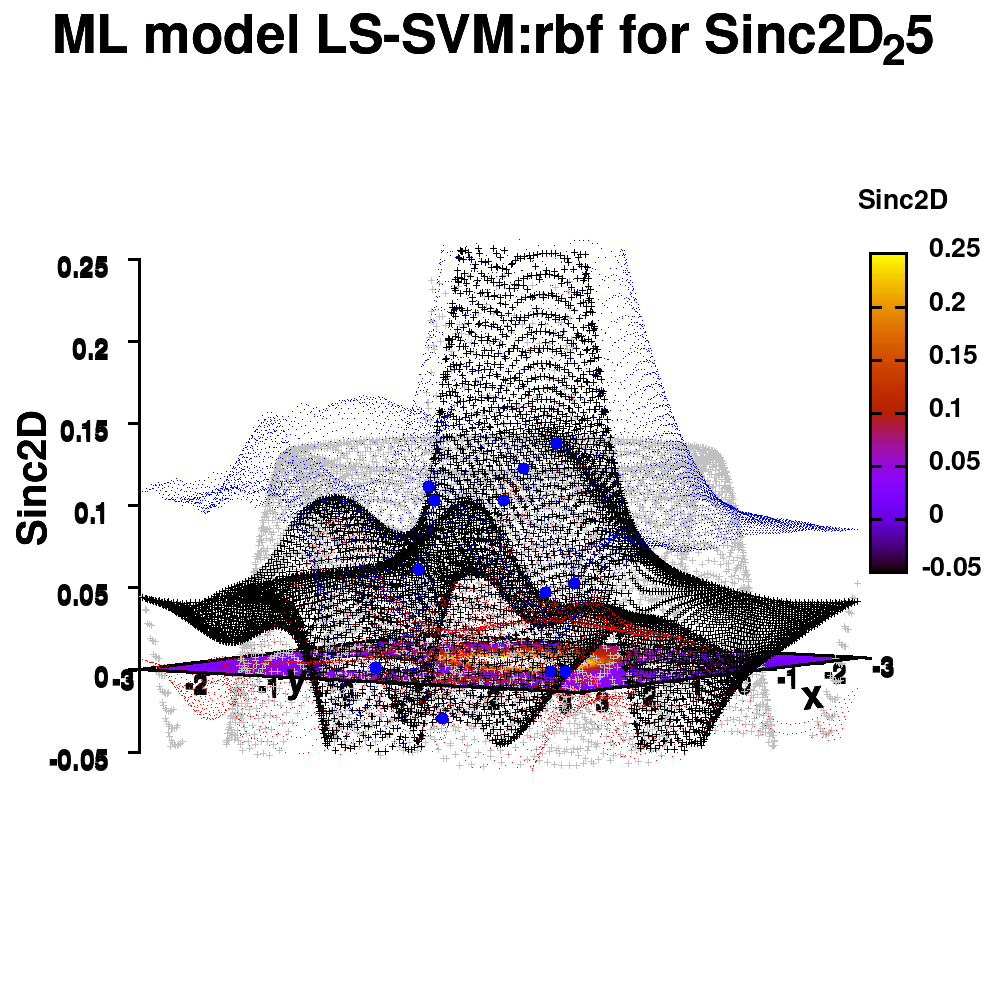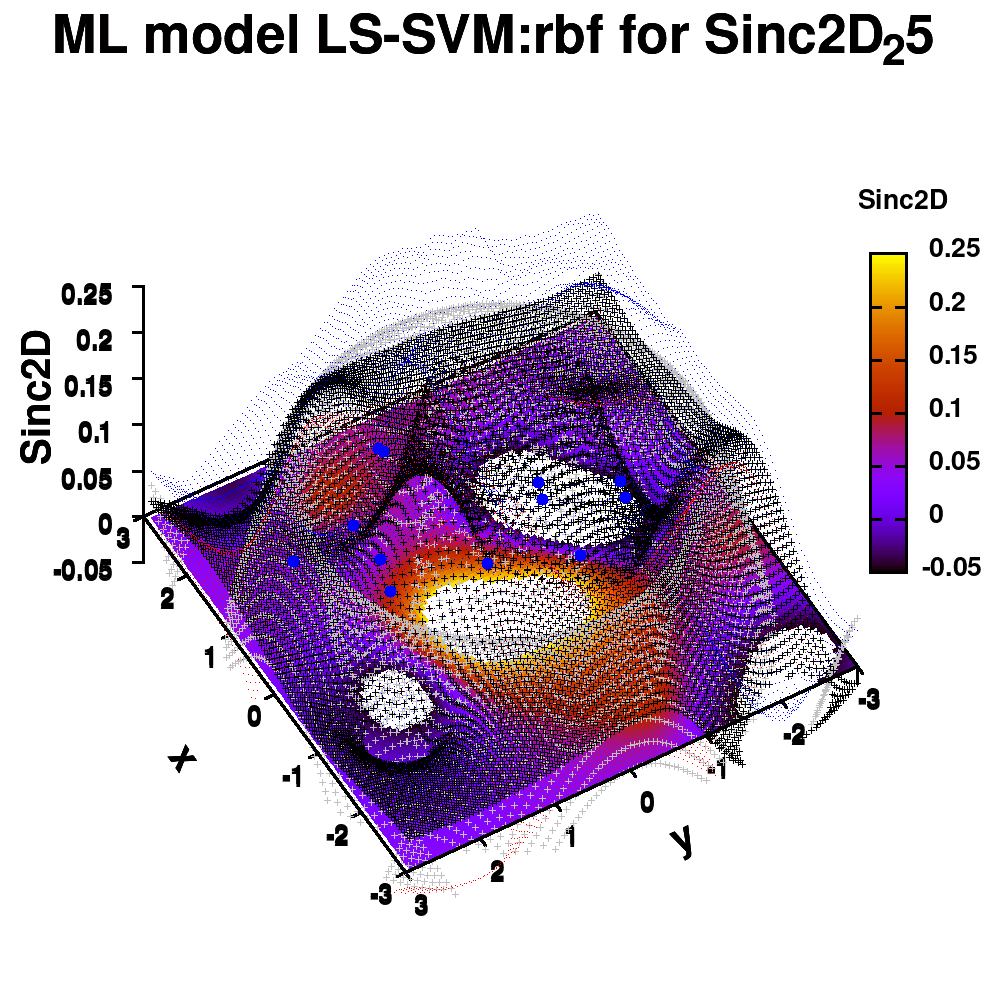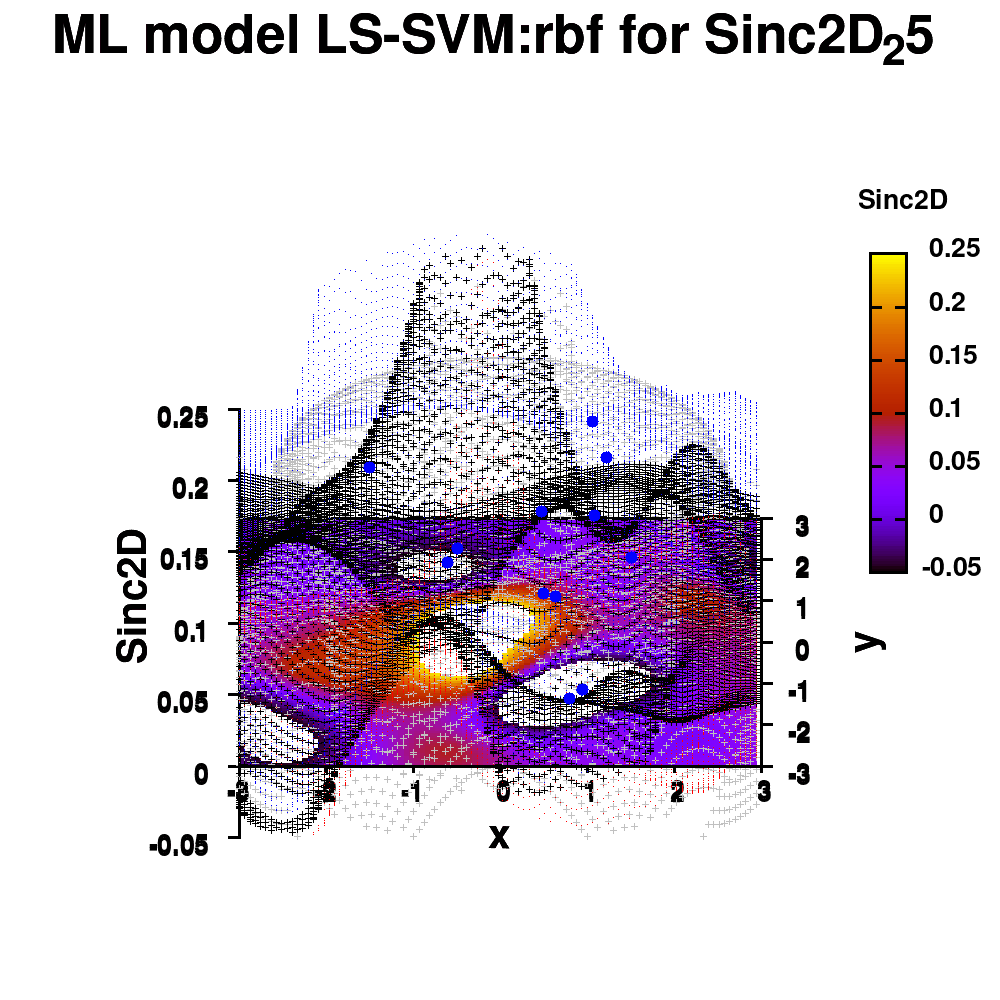
One of the most important aspects in machine-learning—in addition to the modeling itself—is undoubtedly visualization. This can be of either the data set itself or the resulting model. When dealing with small or sparse data sets and a limited number of features, visualization can be extremely helpful to get a feel for your model and data. In this tutorial, we show how you can use gnuplot to generate interesting animations of your data, such as the example above.
What do you need?
- Install Gnuplot version 5.2.8 (or higher) for your OS (under windows you can also install it under your Cygwin installation)
- A data set as a simple multi-column text-file data.dat .
- A similar text-file, model.dat, with your model calculated on a grid .
1. Starting simple: a static image
The main difference between an animation and a static image is the fact the former is just a series of such static images shown one after the other.
1.a. Basic image
Gnuplot allows both interactive and scripted command-line usage. The commands used in interactive mode can simply be placed in a text-file (e.g., myplot.gpl) and run using the command:
> gnuplot myplot.gpl
Comments can be added in such a file by preceding them with a single “#“. In the examples below, I’m using “###” as a personal choice. It shows clearly the location of the comments, and also gives me an easy way to distinguish with script lines I commented out for testing purposes, in which case I use a single #. In the following I also indicate gnuplot commands in red, while options are indicated in turquise. Let u start by plotting the data set in a simple png:
### Set the output to a png file set termopt enhanced set terminal pngcairo size 300,300 font "Helvetica-Bold,6" ### The file to write to set output 'modelplot_v1.png' ### The Title label set title 'ML model tutor' font "Helvetica-Bold,10" splot "data.dat" u 1:2:3
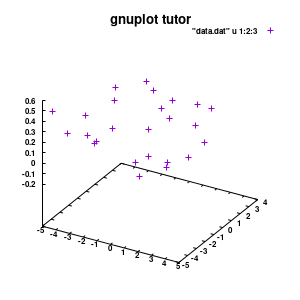
Model v1
With this we set the output to be a png image of 300×300 pixels. (Note: pngcairo also provides png-functionality using the cairo-library. For more complex plotting, it gives much nicer images.) The default font for text is set to “Helvetical-Bold” with a font-size of 6pt. The enhanced option further allows us to use LaTeX type strings, for example indicating subscripts as A_n to print An. The resulting image is stored as ‘modelplot_v1.png‘.
The last two commands are used to create the actual plot. With set title a title can be added to the graph. The default font is replaced in this case by a slightly larger version of 10pt. The splot command allows you to plot 3D surfaces using the same basic information as the gnuplot plot command for 2D plots. In this case, I used the first 3 columns of the data.dat file to plot 3D data, with the x:y:z giving the respective column numbers. The result is shown on the right.
NOTE: An important point to consider is the fact that the font size is absolute. So if you decide later-on to change your image size to say 500×500 pixels, your text labels may look rather small, and you will have to tweak the font-size to compensate of this behavior. Therefore, it is important to make sure you start with the right image size straight away. The 300×300 pixels used in this tutorial are too small for any scientific quality image, it was chosen to be a suitable image size to incorporate in this blog.
1.b. Pimp the axis
With the basics for the graph set up, we can start setting up the graph to our liking.
###settings for the boxplot
set xlabel "M_{n polyX} (g/mol)" offset 0,-1,0 font "Helvetica-Bold, 8" rotate parallel
set xrange[1000:10000] noreverse writeback
set xtics 2000,2000,10000 out scale 1.0 nomirror offset 0,-0.5,0
set ylabel "Graft (%)" offset 2,0,0 font "Helvetica-Bold, 8" rotate parallel
set yrange[0:30] noreverse writeback
set ytics 0,10,30 out scale 1.0 nomirror offset 0,-0.5,0
set zlabel "Particle size (nm)" offset 1,1,0 font "Helvetica-Bold, 8" rotate parallel
set zrange[0:300] noreverse writeback
set ztics 0,50,300 out scale 1.0 nomirror offset 0,-0.5,0
set xyplane at 0
set border lw 3
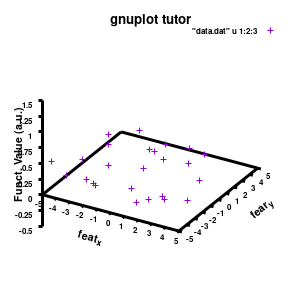
Model v2
The label of each of the three axes can be modified individually using set {x/y/z}label followed by the same options available to any other string (such as the graph title earlier). Here you can see how the enhanced mode allows the use of a subscript using standard LaTeX formatting. The offset makes sure the axis-label does not overlap with the tick-labels. Gnuplot also allows you to define the range to be plotted using set {x/y/z}range[min:max], while set {x/y/z}tics gives you access to the specifics of the individual tics. The latter can be very useful to manually add specific tics, or, as in the current case, manually set the splitting between the different tics. The out option places the tic-marks at the outside of the graph, and their size is set by the scale option.
The command set xyplane can be used to set the intercept of the xy-plane and the z-axis, and set border gives access to the axis-line properties. Here I have set the line-width (lw) to 3.
1.c. Add the (machine-learning) model
Now that the basics properties of the 3D graph are alright*, let us add the model to the plot. This can easily be done by just adding additional input for the splot command.
splot \
"data.dat" using 1:2:3 with points pointtype 7 pointsize 1 linecolor rgb "brown4" notitle, \
"model.dat" u 1:2:3 w line lc rgb "sea-green" notitle
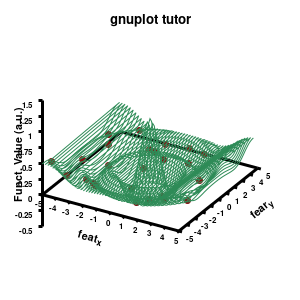
Model v3
The “\” can be used to split the command to multiple lines. In this case, each curve/surface/data set is set on a separate line. Since the command for a single plot can become very long, gnuplot also has a shorthand for most common keywords/options it uses. For the data the extended keywords are shown, and the shorthand is used for the model. The length of the command becomes significantly shorter, but at the same time harder to read. (Note that both shorthand as longhand keywords can be mixed in a single command.)
The data set is now being shown as points, using the 7th pointtype (which are discs). The size of these symbols is set to 1 and the linecolor is a predefined color used by gnuplot. Finally, the notitle option removes the legend entry of this curve. The model data is presented as a line-surface. The end result is shown on the right.
1.d. A better surface-plot: Multi-plot
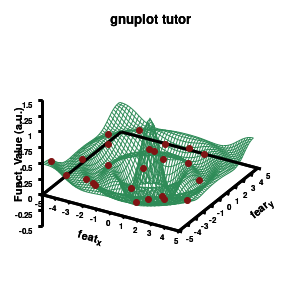
Model v4
As you can see in the previous version of the plot, the model data is plotted as a surface, but this is not a very nice surface. This is because gnuplot just connected the sequential points in the file as a single very long and very complex curve. If you would rotate this plot, it would become clear, several things are very wrong. Luckily there is a very simple solution. Gnuplot has the ability to transform a point-cloud into a surface. This is done by setting a 3D grid using set dgrid3d X,Y. This creates a 3D surface for which the nodes are interpolated between the points of your point-cloud. When you set this option, it is applied on all data curves you plot (i.e., including the set of data-points, which we would like to avoid.). Using the multiplot option of gnuplot the two curves can be drawn separately, using different settings. In the script the splot command is replaced by:
### switch to a multiplot
set multiplot
set dgrid3d 50, 50
splot \
"model.dat" u 1:2:3 w line lc rgb "sea-green" notitle
unset dgrid3d
splot \
"data.dat" using 1:2:3 with points pointtype 7 pointsize 1 linecolor rgb "brown4" notitle
unset multiplot
By setting the multiplot environment, we can unset dgrid3d before drawing the second data set. At the end of script we also unset multiplot to switch of the multiplot environment. At this point it become interesting to see the impact of the terminal pngcairo over png.
1.e. Surface coloring
Drawing a surface is nice, but you can also give it some color. Either by using the z-value as a color scale, or by using another metric/feature to color the surface.
###settings for the color scale
set colorbox vertical
set cblabel "Colormap\n (RGB)" font "Helvetica-Bold, 8" offset -6.75,8 rotate by 0
set pm3d at s explicit
splot \
"model.dat" u 1:2:3 w pm3d notitle
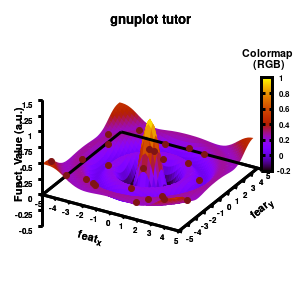
Model v5
Surface coloring is switched on via the command set pm3d which is set at the surface, and is used in splot at the with option. In addition to surface coloring also a color scale is added, with the label formatted using the same options as for other labels. To get the label above the color scale it needs to be shifted using the offset and the rotate option.
The result is rather fancy, but for practical purposes, the surface may actually block the view of the data points. This can be avoided by projecting the color on the xy-plane and retaining a grid representation of the surface. This is done by setting pm3d at the bottom.
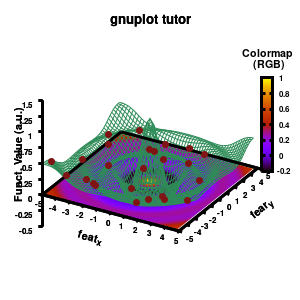
Model v6
In addition, we also need to plot the model surface twice, once to generate the color map and once to generate the model surface as a grid-image.
set pm3d at b explicit
splot \
"model.dat" u 1:2:3 w pm3d notitle,\
"model.dat" u 1:2:3 w line lc rgb "sea-green" notitle
2. Creating an animation
With gnuplot it is quite easy to generate stunning 3D animated gif images. Some nice examples can be found all over the web, such as this animated Bessel function, my own (very old) molecular d-and f-orbitals, or this collection. Once you finish creating a script to generate a single image, creating an animation requires only some minor modifications. First of all we need to select the correct terminal (i.e., gif instead of png)
set terminal gif transparent animate nooptimize delay 10 size 300,300 font "Helvetica-Bold,10" set output 'modelplot_v7.gif'
This generates a transparent animated gif with a delay of 10 ms between frames, and stores it in a gif image. In addition, a change in time/image frame needs to be implemented. This can easily be done by a simple for loop, which is wrapped around the plotting section.
n=60
do for [i=1:n]{
set view 60, i*360/n
### do the multiplot plotting section
set multiplot
...all the other plotting stuff of before
unset multiplot
}
set output
model v7: animated
In the example, the 3D graph is rotated. This is done by changing the view via the set view command which takes two angles in degrees. As you can see from “i*360/n“, gnuplot also accepts simple mathematical equations.
Once the loop is finished we need to close our gif animation. This is done via (a side-effect of) the command set output. The set output {filename} command sets the output to a file with name filename, or if a filename is omitted to the standard output. As a side-effect it closes the current output file, c.q. our animated gif.
An alternative method for creating an animation would be creating a series of images (in the image-format of your choice, e.g. pngcairo and then create an apng) and combining them yourself or via additional scripting into an animated image format using additional software, such as is done here.
3. Animated surfaces and coloring
The example above is rather trivial in regard to animations. The ability to perform math inside a gnuplot script provides you the ability to make things a lot more interesting. In the following, we are going to construct a small imaginary solar system, to present some of the things which are possible.
The basic script for the solar system above can be downloaded here.
set termopt enhanced
set terminal gif animate nooptimize delay 10 size 300,300 font "Helvetica,10"
set output 'Solarplot_v1.gif'
set title 'Magic Solar System' font "Helvetica-Bold,10"
maxl=10
set xrange[-maxl:maxl] noreverse writeback
set yrange[-maxl:maxl] noreverse writeback
set zrange[-maxl:maxl] noreverse writeback
set xyplane at 0
set border lw 1.5
###Use parametric coordinated for plotting spheres
set parametric # enable parametric mode with angles (u,v)
set urange [0:2*pi]
set vrange [-pi/2.0:pi/2.0]
set isosample 360,180
fx(u,v)=cos(u)*cos(v)
fy(u,v)=sin(u)*cos(v)
fz(v)=sin(v)
### Surface coloring
set colorbox vertical
set cblabel "Planet\n colors" font "Helvetia, 8" offset -4.75,5 rotate by 0
set pm3d depthorder base nohidden3d
unset hidden3d
### The animated drawing
n = 60
do for [i=1:n]{
# The star
x=0.0
y=0.0
z=0.0
r=3.0
# The first planet
x1=5.0*sin(i*2*pi/n)
y1=5.0*cos(i*2*pi/n)
z1=0.0
r1=0.50
color1(u,v)=0.5
# The second planet
x2=6.5*sin(i*2*pi/n)
y2=7.0*cos(i*2*pi/n)
z2=1.0*cos(i*2*pi/n)
r2=1.0
color2(u,v)=sin(v)*2*pi
splot \
"++" using (x+r*fx(u,v)):(y+r*fy(u,v)):(z+r*fz(v)):(6.5) w pm3d notitle,\
"++" using (x1+r1*fx(u,v)):(y1+r1*fy(u,v)):(z1+r1*fz(v)):(color1(u,v)) w pm3d notitle,\
"++" using (x2+r2*fx(u,v)):(y2+r2*fy(u,v)):(z2+r2*fz(v)):(color2(u,v)) w pm3d notitle
}
set output
Most of the commands and options have already been covered above. To draw our spherical planets, we introduce a set of parametric coordinates (u,v) via the command set parametric. Next we set their ranges, just as you would do for the x,y, and z coordinates via set {u|v}range. The command set isosample is used to define the grid over the parametric space. With this setup, you can now define any parametric surface you want. In our case, we want to have a sphere. For this we define three transformation functions. With u and v representing the θ and φ angles of a sphere, the transformation to Cartesian coordinates is given by the functions fx(u,v),fy(u,v), and fz(v).
In the main loop of the gif we define the center position (x,y,z) and the radius (r) of our planets and star, with the latter nicely fixed at the origin, and our planets having an orbit around it. To have a nice periodic gif, you should make sure that any periodic behavior ends up where it started, hence the 2pi factor in the sines and cosines. Everything is drawn with a single splot command where we use a pseudo 4-column input style:
(x-coord):(y-coord):(z-coord):(color-coord)
Note that the brackets ‘(‘ & ‘)‘ are important to include as gnuplot will throw errors otherwise. The selected color, can be either a real value in the color scale or a function. The resulting solar system is shown below on the left.
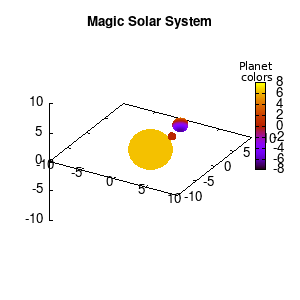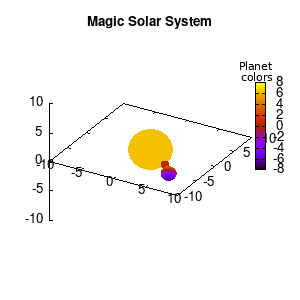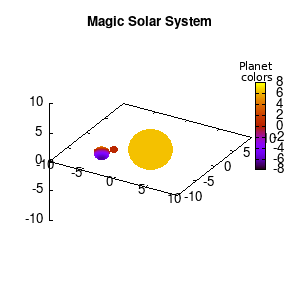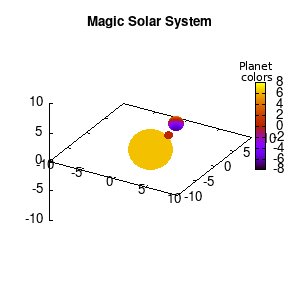 Solar v1, no depth |
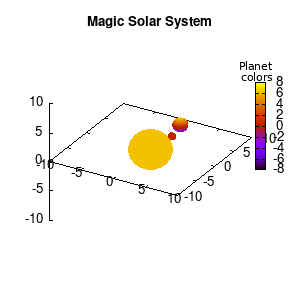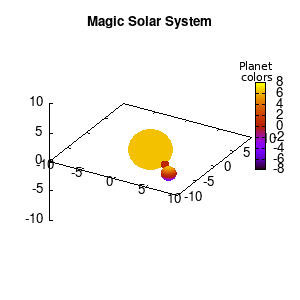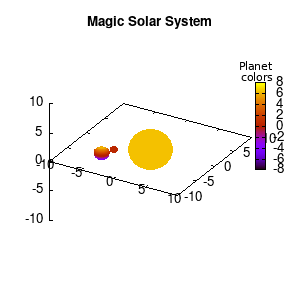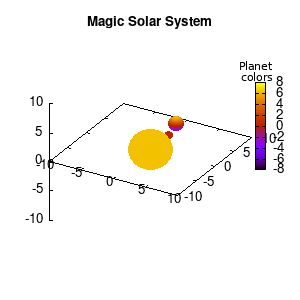 Solar v1, depth |
Not that bad for a first attempt. There is however a small snag: the 3D effect is somehow off when the planets move behind the star. This is due to the depth-buffering. The newest versions of gnuplot (≥5.2.8) provide the option depthorder for the set pm3d command. Using the value base for the depthorder option results in the depthorder to be decided based on the z-projected position of the object. This is sufficient to fix our little solar system, as you can see on the right.
3.a. Some cleanup work: removing the box and complex coloring
As we are creating an imaginary (magical) solar system, we should maybe get rid of the x-,y-, and z-axis. This is done via the commands unset border to get rid of the axis-bars and unset {x|y|z}tics to remove the tic-marks and-labels.
unset border unset xtics unset ytics unset ztics set palette defined (0 "red", 1 "yellow",1 "brown", 2 "brown4",3 "dark-green", 4 "blue", 5 "white") set cbrange[0:10] #unset cbtics
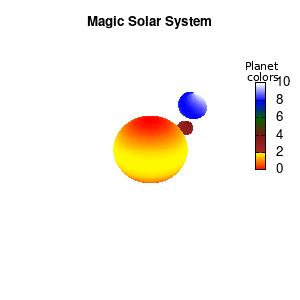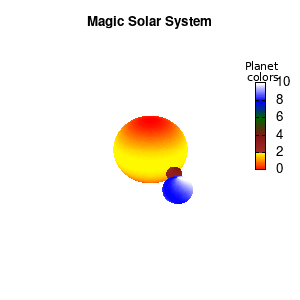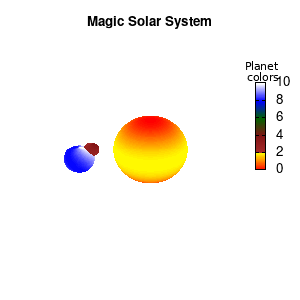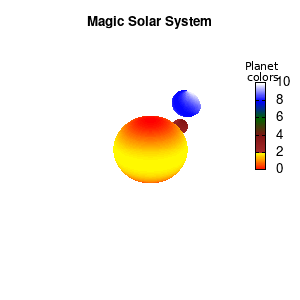
Solar v2
And although the color palette provided is nice, if we want different color schemes on each of the planets, we quickly run into a small problem: you can only have 1 color palette per splot. In case of a static image, you might be able to get around this problem by using a multiplot (as before) and have overlapping splots with each their own palette. But…in that case you will also be responsible for getting the 3D order of your objects correct yourself. And although this may be doable for a single frame, in case of an animated 3D solar system this will be a hassle nearly impossible to overcome**. For this you need to tackle the problem in a different way: create your own color palette consisting of sub-palettes. This can be done via the command set palette defined. The pairs give the color at the endpoints of gradient ranges, with the overall range (here 0-5) representing the entire color scale. The intermediate points are placed equidistant, so for a color range from 0:10 the red-to-yellow gradient is linked to color values in the range 0:2, while the blue-to-white gradient is linked to the color values in the range 8:10. Applying this to our solar system we can give nice individual color palettes to each of the objects. I changed the size and position of the three objects a bit, and as you can see, the outer planet moves outside of the x/y/z-ranges. Now that we know how to add different color palettes to each of our planets, we can also remove the color-bar on the right using the command unset colorbox, remove the tics via unset cbtics, and remove the label via unset cblabel.
3.b. time-dependent colors
We have motion of objects and different color palettes, what about changing the colors during the animation? As we saw earlier, the color component can be defined as a function, which means we can make this time-dependent as well. Let’s imagine that our outer planet is traveling on a rather elliptic orbit, making it heat up when it approaches our star.
# The first planet
color1(u,v)=0.5*(cos(u)**5+sin(v)**3)+sin(i*6*pi/n) +8.0
# The second planet
x2=8+15*sin((i+20)*2*pi/n)
y2=6.0*cos((i+20)*2*pi/n)
z2=3.0*cos((i+20)*2*pi/n)
color2(u,v)=0.99*sin((i+20)*2*pi/n+pi)+1
By making the color dependent on the frame number, the (uniform) coloring of our second planet will now cycle through the red-yellow gradient. The first planet experiences a variation at 3x the speed but have a non-uniform surface coloring.

Solar v3
3.c. time-dependent colors and shapes
Once you have time dependent coloring, and time dependent motion, you can also have time dependent shapes and combine all three. This is all possible within the same basic framework set up above. For example, we can make our star a bit more active, letting it bulge and swirl. Adding another planet and some moons the magic solar system below is created by this gnuplot script.

Solar v4
4. Conclusion
Gnuplot provides a versatile tool for creating animated gifs of your machine learning data and models, or anything else you could imagine. It has an extensive number of options which allow you to tweak each single property of your graph. The ability to perform simple arithmetic within a gnuplot-script further increases the potential.
* Ignore the rather crummy quality of the embedded images. This is an artifact of only having a 300×300 pixel image, the animation at the top of the page has an 1000×1000 pixel resolution and shows a much better quality.
** Of course with enough persistence you may find a way to get it done…but there are less sadomasochistic ways of doing this 😉
Permanent link to this article: https://dannyvanpoucke.be/tut-gnuplot-gifs-machine-learning/
Aug 16 2020
Building your own scikit-learn Regressor-Class: LS-SVM as an example
The world of Machine-Learning (ML) and Artificial Intelligence (AI) is governed by libraries, as the implementation of a full framework from scratch requires a lot of work. ML and data-science engineers and researchers, therefore don’t generally build their own libraries. Instead they use and extend existing libraries written in python or R. One of the most popular current python ML libraries is scikit-learn. This library provides access to scores of ML-models and methods which can be combined at will via the use of a consistent global API.
However, no matter how many models there are included in such a library, chances are that a model you wish to use (or the extension you envision for an existing model) is not implemented. In such a case, you do not want to write an entire ML framework from scratch, but just create your own model and fit it into the existing framework. Within the scikit-learn framework this can be done with relative ease, as is explained in this short tutorial. As an example, I will be building a regressor class for the LS-SVM model.
1. The ML-model: LS-SVM?
Least-Squares Support Vector Machines is a type of support vector machines (SVM) initially developed some 20 years ago by researchers at the KULeuven (and is still being further developed, funded via several ERC grants). It’s a supervised learning machine learning approach in which a system of linear equations is solved using the kernel-trick.
So how does it work in practice? Assume, we have a data set of data points (xi,yi), with xi the feature vector and yi the target of the data point (or sample) i. Depending on whether you want to perform classification or regression, training the model corresponds to solving the following system of equations (represented in their matrix form as):
Classification:
Regression:
with the vector containing all targets yi,
a hyperparameter, and
a kernel function
.
Once trained, results are predicted (in case of regression) by solving the following equation:
More details on these can be found in the book of Suykens, or (if you prefer a shorter read) this paper by Dilmen.
The above model is available through the Matlab library developed by the Suykens group, and has been translated to R, but no implementation in the python scikit-learn library is available, therefore we set out to create such an implementation following the scikit-learn API. Our choice to follow the scikit-learn API is twofold: (1) we want our new class to smoothly integrate with the functionalities of the scikit-learn library (I’m building a framework for automated machine learning on this library, hence all my models need to show the same behavior and functionality) and (2) we want to be lazy and implement as little as possible.
2. Creating a Simple Regressor Class.
2.1. Initialization
Designing this Class, we will make full use of OOP (Similar ideas as in my fortran tutorials), inheriting behavior from scikit-learn base classes. All estimators in scikit-learn are derived from the BaseEstimator Class. The use of this class requires you to define all parameters of your class as keyword arguments in the __init__ function of your class. In return, you get the get_params and set_params methods for free.
As our goal is to create a regressor class, the class also needs to inherit from the RegressorMixin Class which provides access to the score method used by all scikit-learn regressors. With this, the initial implementation of our LS-SVM regressor class quickly takes shape:
class LSSVMRegression(BaseEstimator, RegressorMixin): """ An Least Squared Support Vector Machine (LS-SVM) regression class Attributes: - gamma : the hyper-parameter (float) - kernel: the kernel used (string: rbf, poly, lin) - kernel_: the actual kernel function - x : the data on which the LSSVM is trained (call it support vectors) - y : the targets for the training data - coef_ : coefficents of the support vectors - intercept_ : intercept term """ def __init__(self, gamma:float=1.0, kernel:str=None, c:float=1.0, d:float=2, sigma:float=1.0): self.gamma=gamma self.c=c self.d=d self.sigma=sigma if (kernel is None): self.kernel='rbf' else: self.kernel=kernel params=dict() if (kernel=='poly'): params['c']=c params['d']=d elif (kernel=='rbf'): params['sigma']=sigma self.kernel_=LSSVMRegression.__set_kernel(self.kernel,**params) self.x=None self.y=None self.coef_=None self.intercept_=None
All parameters have a default value in the __init__ method (and with a background in Fortran, I find it very useful to explicitly define the intended type of the parameters). Additionally, the same name is used for the attributes to which they are assigned. The kernel function is provided as a string (here we have 3 possible kernel functions: the linear (lin), the polynomial (poly), and the radial basis function (rbf) ) and linked to a function pointer via the command:
self.kernel_=LSSVMRegression.__set_kernel(self.kernel,**params)
The static private __set_kernel method returns a pointer to the correct kernel-function, which is later-on used during training and fitting. The get_params, set_params, and score methods, we get for free so no implementation is needed, but you could override them if you wish. (Note that some tutorials recommend against overriding the get_params and set_params methods.)
2.2. Fitting and predicting
As our regressor class should be interchangeable with any regressor class available by scikit-learn, we look at some examples to see which method-names are being used for which purpose. Checking the LinearRegression model and the SVR model, we learn that the following methods are provided for both classes:
| method | task | LS-SVM class |
|---|---|---|
| __init__ | Initialize object of the class. | Implemented above (ourselves) |
| get_params | Get a dictionary of class parameters. | Inherited from BaseEstimator |
| set_params | Set the class parameters via a dictionary. | Inherited from BaseEstimator |
| score | Return the R2 value of the prediction. | Inherited from RegressorMixin |
| fit | Fit the model. | to do |
| predict | Predict using the fitted model. | to do |
Only the fit and predict methods are still needed to complete our LS-SVM regressor class. The implementation of the equations presented in the previous section can be done in a rather straight forward way using the numpy library.
import numpy as np def fit(self,X:np.ndarray,y:np.ndarray): self.x=X self.y=y Omega=self.kernel_(self.x,self.x) Ones=np.array([[1]]*len(self.y)) A_dag = np.linalg.pinv(np.block([ [0, Ones.T ], [Ones, Omega + self.gamma**-1 * np.identity(len(self.y))] ])) B = np.concatenate((np.array([0]),self.y), axis=None) solution = np.dot(A_dag, B) self.intercept_ = solution[0] self.coef_ = solution[1:] def predict(self,X:np.ndarray)->np.ndarray: Ker = self.kernel_(X,self.x) Y=np.dot(self.coef_,Ker.T) +self.intercept_ return Y
Et voilà, all done. With this minimal amount of work, a new regression model is implemented and capable of interacting with the entire scikit-learn library.
3. Getting the API right: Running the Model using Scikit-learn Methods.
The LS-SVM model has at least 1 hyperparameter: the factor and all hyperparameters present in the kernel function (0 for the linear, 2 for a polynomial, and 1 for the rbf kernel). To optimize the hyperparameters, the GridsearchCV Class of scikit-learn can be used, with our own class as estimator.
For the LS-SVM model, which is slightly more complex than the trivial examples found in most tutorials, you will encounter some unexpected behavior. Assume you are optimizing the hyperparameters of an LS-SVM with an rbf kernel: and
.
from sklearn.model_selection import GridSearchCV ... parameters = {'kernel':('rbf'), 'gamma':[0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0], 'sigma':[0.001, 0.01, 0.1, 1.0, 10.0, 100.0, 1000.0]} lssvm = LSSVMRegression() clf = GridSearchCV(lssvm, parameters) clf.fit(X, y) ...
When you plot the quality results as a function of , you’ll notice there is very little (or no) variation with regard to
. Some deeper investigation shows that the instances of the LSSVMRegression model use different values of the
attribute, however, the
attribute does not change in the kernel function. This behavior is quite odd if you expect the GridsearchCV class to create a new class instance (or object) using the __init__ method for each grid point (a natural assumption within the context of parallelization). In contrast, the GridsearchCV class appears to be modifying the attributes of a set of instances via the set_params method, as can be found in the 2000+ page manual of scikit-learn, or here in the online manual:

Scikit-learn manual section of parameter initialization of classes
In programming languages like C/C++ or Fortran, some may consider this as bad practice as it entirely negates the use of your constructor and splits the initialization section. For now, we will consider this a feature of the Python scripting language. This also means that getting a static class function linked to the kernel_ attribute requires us to override the get_params method (initializing attributes in a fit function is just a bridge too far 😉 ).
def set_params(self, **parameters): for parameter, value in parameters.items(): setattr(self, parameter, value) params=dict() if (self.kernel=='poly'): params['c']=self.c params['d']=self.d elif (self.kernel=='rbf'): params['sigma']=self.sigma self.kernel_=LSSVMRegression.__set_kernel(self.kernel,**params) return self
For consistency the get_params method is also overridden. The resulting class is now suitable for use in combination with the rest of the scikit-learn library.
4. The LS-SVM Regressor on Github
At the moment of witting no LS-SVM regressor class compatible with the scikit-learn library was available. There are some online references available to Python libraries which claim to have the LS-SVM model included, but these tend to be closed source. So instead of trying to morph these to fit my framework, I decided to use this situation as an opportunity to learn some more on the implementation of an ML model and the integration of this model in the scikit-learn framework. The resulting model is extended further to deal with the intricacies of my own framework aimed at small datasets, which is beyond the scope of the current tutorial. Since I believe the LS-SVM regressor may be of interest to other users of the scikit-learn library, you can download it from my github-page:
<LSSVMlib>
5. References
- J.A.K. Suykens et al., “Least Squares Support Vector Machines“, World Scientific Pub. Co., Singapore, 2002 (ISBN 981-238-151-1)
- E. Dilmen and S. Beyhan, “A Novel Online LS-SVM Approach for Regression and Classification”, IFAC-PapersOnLine Volume 50(1), 8642-8647 (2017)
- D. Hnyk, “Creating your own estimator in scikit-learn“, webpage
- T. Book, “Building a custom model in scikit-learn“, webpage
- “User guide: create your own scikit-learn estimator“, webpage
DISCLAIMER: Since Python codes depreciate as fast as they are written, links to the scikit-learn library documentation may be indicated as outdated by the time you read this tutorial. Check out the most recent version in that case. Normally, the changes should be sufficiently limited not to impact the conclusions drawn here. However, if you discover a code-breaking update, feel free to mention it here in the comments section.
Permanent link to this article: https://dannyvanpoucke.be/building-scikit-learn-regressor-lssvm-en/
Aug 09 2020
Parallel Python in classes…now you are in a pickle
In the past, I discussed how to create a python script which runs your calculations in parallel. Using the multiprocessing library, you can circumvent the GIL and employing the async version of the multiprocessing functions, calculations are even performed in parallel. This works quite well, however, when using this within a python class you may run into some unexpected behaviour and errors due to the pickling performed by the multiprocessing library.
For example, if the doOneRun function is a class function defined as
class MyClass:
...
def doOneRun(self, id:int):
return id**3
...
and you perform some parallel calculation in another function of your class as
class MyClass:
...
def ParallelF(self, NRuns:int):
import multiprocessing as mp
nproc=10
pool=mp.Pool(processes=nprocs)
drones=[pool.apply_async(self.doOneRun, args=(nr,)) for nr in range(NRuns)]
for drone in drones:
Results.collectData(drone.get())
pool.close()
pool.join()
...
you may run into a runtime error complaining that a function totally unrelated to the parallel work (or even to the class itself) can not be pickled. 😯
So what is going on? In the above setup, you would expect the pool.apply_async function to take just a function pointer to the doOneRun function. However, as it is provided by a the call self.doOneRun, the pool-function grabs the entire class and everything it contains, and tries to pickle it to distribute it to all the processes. In addition to the fact that such an approach is hugely inefficient, it has the side-effect that any part associated to your class needs to be pickleable, even if it is a class-function of a class used to generate an object which is just a property of the MyClass Class above.
So both for reasons of efficiency and to avoid such side-effects, it is best to make the doOneRun function independent of a class, and even placing it outside the class.
def doOneRun(id:int):
return id**3
class MyClass:
...
def ParallelF(self, NRuns:int):
import multiprocessing as mp
nproc=10
pool=mp.Pool(processes=nprocs)
drones=[pool.apply_async(doOneRun, args=nr) for nr in range(NRuns)]
for drone in drones:
Results.collectData(drone.get())
pool.close()
pool.join()
...
This way you avoid pickling the entire class, reducing initialization times of the processes and the unnecessary communication-overhead between processes. As a bonus, you also reduce the risk of unexpected crashes unrelated to the calculation performed.
Permanent link to this article: https://dannyvanpoucke.be/parallel-python-classes-pickle/
Aug 04 2020
Practical Machine-Learning for the Materials Scientist
Individual model realizations may not perform that well, but the average model realization always performs very well.
Machine-Learning is up and trending. You can’t open a paper, magazine or website without someone trying to convince you their new AI-improved app/service will radically change your life. It will make the production of your company more efficient and cheaper, make costumers flock to your shop and possibly cure cancer on the side. Also in science, a lot of impressive claims are being made. General promises entail that it makes the research of interest faster, better, more efficient,… There is, however, a bit of fine print which is never explicitly mentioned: you need a LOT of data. This data is used to teach your Machine-Learning algorithm whatever it is intended to learn.
In some cases, you can get lucky, and this data is already available while in other, you still need to create it yourself. In case of computational materials science this often means performing millions upon millions of calculations to create a data set on which to train the Machine-Learning algorithm.[1] The resulting Machine-Learning model may be a thousand times faster in direct comparison, but only if you ignore the compute-time deficit you start from.
In materials science, this is not only a problem for those performing first principles modeling, but also for experimental researchers. When designing a new material, you generally do not have the resources to generate thousands or millions of samples while varying the parameters involved. Quite often you are happy if you can create even a few dozen samples. So, can this research still benefit from Machine-Learning if only very small data sets are available?
In my recent work on materials design using Machine-Learning combined with small data sets, I discuss the limitations of small data sets in the context of Machine-Learning and present a natural approach for obtaining the best possible model.[2] [3]
The Good, the Bad and the Average.
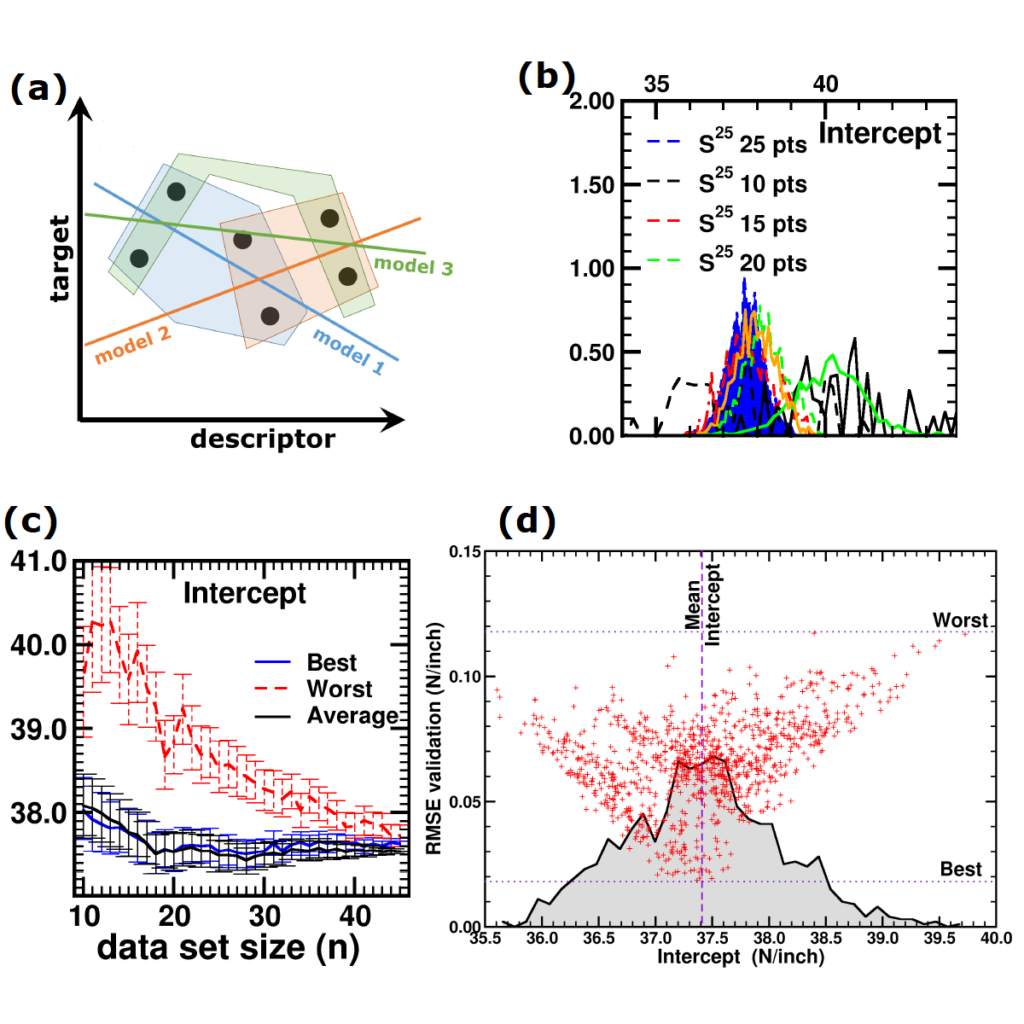
(a) Simplified representation of modeling small data sets. (b) Data set size dependence of the distribution of model coefficients. (c) Evolution of model-coefficients with data set size. (d) correlation between model coefficient value and model quality.
In Machine-Learning a data set is generally split in two parts. One part to train the model, and a second part to test the quality of the model. One of the underlying assumptions to this approach is that each subset of the data set provides an accurate representation of the “true” data/model. As a result, taking a different subset to train your data should give rise to “the same model” (ignoring small numerical fluctuations). Although this is generally true for large (and huge) data sets, for small data sets this is seldomly the case (cf. figure (a) on the side). There, the individual data points considered will have a significant impact on the final model, and different subsets give rise to very different models. Luckily the coefficients of these models still present a peaked distribution. (cf. figure (b)).
On the down side, however, if one isn’t careful in preprocessing the data set correctly, these distributions will not converge upon increasing the data set size, giving rise to erratic model behaviour.[2]
Not only the model coefficients give rise to a distribution, the same is true for the model quality. Using the same data set, but making a different split between training and test data can give rise to large differences in quality for the model instances. Interestingly, the model quality presents a strong correlation with the model coefficients, with the best quality model instances being closer to the “true” model instance. This gives rise to a simple approach: just take many train-test splittings, and select the best model. There are quite some problems with such an approach, which are discussed in the manuscript [2]. The most important one being the fact that the quality measure on a very small data set is very volatile itself. Another is the question of how many such splittings should be considered? Should it be an exhaustive search, or are any 10 random splits good enough (obviously not)? These problems are alleviated by the nice observation that “the average” model shows not the average quality or the average model coefficients, but instead it presents the quality of the best model (as well as the best model coefficients). (cf. figure (c) and (d))
This behaviour is caused by the fact that the best model instances have model coefficients which are also the average of the coefficient distributions. This observation hold for simple and complex model classes making it widely applicable. Furthermore, for model classes for which it is possible to define a single average model instance, it gives access to a very efficient predictive model as it only requires to store model coefficients for a single instance, and predictions only require a single evaluation. For models where this is not the case one can still make use of an ensemble average to benefit from the superior model quality, but at a higher computational cost.
References and footnotes
[1] For example, take “ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost“, one of the most downloaded papers of the journal of Chemical Science. The data set the authors generated to train their neural network required them to optimize 58.000 molecules using DFT calculations. Furthermore, for these molecules a total of about 17.200.000 single-point energies were calculated (again at the DFT level). I leave it to the reader to estimate the amount of calculation time this requires.
[2] “Small Data Materials Design with Machine Learning: When the Average Model Knows Best“, Danny E. P. Vanpoucke, Onno S. J. van Knippenberg, Ko Hermans, Katrien V. Bernaerts, and Siamak Mehrkanoon, J. Appl. Phys. 128, 054901 (2020)
[3] “When the average model knows best“, Savannah Mandel, AIP SciLight 7 August (2020)
Permanent link to this article: https://dannyvanpoucke.be/practical-machine-learning/
Aug 04 2020
Small Data Materials Design with Machine Learning: When the Average Model Knows Best
| Authors: | Danny E. P. Vanpoucke, Onno S. J. van Knippenberg, Ko Hermans, Katrien V. Bernaerts, and Siamak Mehrkanoon |
| Journal: | Journal of Applied Physics 128, 054901 (2020) |
| doi: | 10.1063/5.0012285 |
| IF(2019): | 2.286 |
| export: | bibtex |
| pdf: | <JApplPhys> (Open Access) |
| github: | <Amadeus> |
 |
| Graphical Abstract: Correlation plot of the RMSE of the validation set and the intercept value for linear model instances trained on 1000 subsets of a 25 point data set. The distribution of the correlation data is indicated by the black curve. |
Abstract
Machine Learning is quickly becoming an important tool in modern materials design. Where many of its successes are rooted in huge data sets, the most common applications in academic and industrial materials design deal with data sets of at best a few tens of data points. Harnessing the power of Machine Learning in this context is therefore of considerable importance. In this work, we investigate the intricacies introduced by these small data sets. We show that individual data points introduce a significant chance factor in both model training and quality measurement. This chance factor can be mitigated by the introduction of an ensemble-averaged model. This model presents the highest accuracy while at the same time it is robust with regard to changing data set size. Furthermore, as only a single model instance needs to be stored and evaluated, it provides a highly efficient model for prediction purposes, ideally suited for the practical materials scientist.
Permanent link to this article: https://dannyvanpoucke.be/paper_averagemodel-en/
Dec 27 2019
Parallel Python?
As part of my machine learning research at AMIBM, I recently ran into the following challenge: “Is it possible to do parallel computation using python.” It sent me on a rather long and arduous journey, with the final answer being something like: “very reluctantly“.
Python was designed with one specific goal in mind; make it easy to implement small test programs to see if an idea is worth pursuing. This gave rise to a scripting language with a lot of flexibility, but also with significant limitations, most of which the “intended” user would never meet. However, as a consequence of its success, many are using it going far beyond this original scope (yours truly as well 🙂 ).
Python offers various libraries to parallelize your scripts…most of them wrappers adding minor additional functionality. However, digging down to the bottom one generally ends up at one of the following two libraries: the threading module and the multiprocessing module.
Of course, as with many things python, there is a huge amount of tutorials available with many of great quality.
import threading
Programmers experienced in a programming language such as C/C++, Pascal, or Fortran, may be familiar with the concept of multi-threading. With multi-threading, a CPU allows a program to distribute its work over multiple program-threads which can be performed in parallel by the different cores of the CPU (or while a core is idle, e.g., since a thread is waiting for data to be fetched). One of the most famous API’s for writing multi-threaded applications is OpenMP. In the past I used it to parallelize my Hirshfeld-I implementation and the phonon-module of HIVE.
For Python, there is no implementation of the OpenMP API, instead there is the threading module. This provides access to the creation of multiple threads, each able to perform their own tasks while sharing data-objects. Unfortunately, python has also the Global Interpreter Lock, GIL for short, which allows only a single thread to access the interpreter at a time. This effectively reduces thread-based parallelization to a complex way of running a code in a serial way.
For more information on “multi-threading” in python, you can look into this tutorial.
import multiprocessing
In addition to the threading module, there is also the multiprocessing module. This module side-steps the GIL by creating multiple processes, each having its own interpreter. This however comes at a cost. Firstly, there is a significant computational cost starting the different processes. Secondly, objects are not shared between processes, so additional work is needed to collect and share data.
Using the “Pool” class, things are somewhat simplified, as can be seen in the code-fragment below. With the pool class one creates a set of threads/processes available for your program. Then through the function apply_async function it is possible to run processes in parallel. (Note that you need to use the “async” version of the function, as otherwise you end up with running things serial …again)
- import multiprocessing as mp
-
- def doOneRun(id:int): #trivial function to run in parallel
- return id**3
-
-
-
- num_workers=10 #number of processes
- NRuns=1000 #number of runs of the function doOneRun
-
- pool=mp.Pool(processes=num_workers) # create a pool of processes
- drones=[pool.apply_async(doOneRun, args=nr) for nr in range(NRuns)] #and run things in parallel
-
- for drone in drones: #and collect the data
- Results.collectData(drone.get()) #Results.collectData is a function you write to recombine the separate results into a single result and is not given here.
-
- pool.close() #close the pool...no new tasks can be run on any of the processes
- pool.join() #collapse all threads back into the main thread
how many cores does my computer have?
If you are used to HPC applications, you always want to get as much out of your machine as possible. With regard to parallelization this often means making sure no CPU cycle is left unused. In the example above we manually selected the number of processes to spawn. However, would it not be nice if the program itself could just set this value to be equal to the number of physical cores accessible?
Python has a large number of functions claiming to do just that. A few of them are given below.
- multiprocessing.cpu_count(): returns the number of logical cores it can find. So if you have a modern machine with hyper-threading technology, this will return a multiple of the number of physical cores (and you will be over-subscribing your CPU.
- os.cpu_count(): same as multiprocessing.cpu_count().
- psutil.cpu_count(logical=False): This implementation gives the same default behavior, however, the parameter logical allows for this function to return the correct number of cores in a single CPU. Indeed a single CPU. HPC architectures which contain multiples CPUs per node will again return an incorrect number, as the implementation makes use of a python “set”, and as such doesn’t increment for the same index core on a different CPU.
In conclusion, there seems to be no simple way to obtain the correct number of physical cores using python, and one is forced to provide this number manually. (If you do have knowledge of such a function which works in both windows and unix environments and both desktop and HPC architectures feel free to let me know in the comments.)
All in all, it is technically possible to run code in parallel using python, but you have to deal with a lot of python quirks such as GIL.
Permanent link to this article: https://dannyvanpoucke.be/parallel-python-en/
- 1
- 2