Today we had our fourth consortium meeting for the DigiLignin project. Things are moving along nicely, with a clear experimental database almost done by VITO, the Machine Learning model taking shape at UMaastricht, and quantum mechanical modeling providing some first insights.
Permanent link to this article: https://dannyvanpoucke.be/digilignin-c4-en/
Mar 06 2024
First-principles investigation of hydrogen-related reactions on (100)–(2×1)∶H diamond surfaces
| Authors: | Emerick Y. Guillaum, Danny E. P. Vanpoucke, Rozita Rouzbahani, Luna Pratali Maffei, Matteo Pelucchi, Yoann Olivier, Luc Henrard, & Ken Haenen |
| Journal: | Carbon 222, 118949 (2024) |
| doi: | 10.1016/j.carbon.2024.118949 |
| IF(2022): | 10.9 |
| export: | bibtex |
| pdf: | <Carbon> |
 |
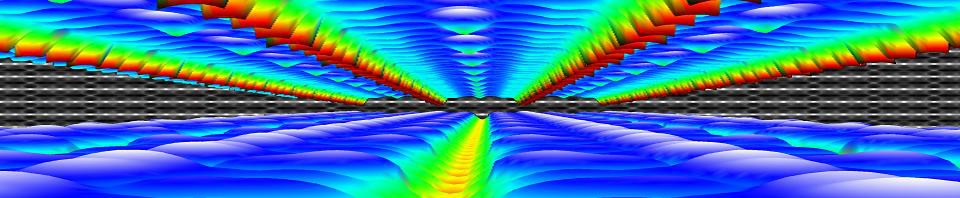
| Graphical Abstract: (left) Ball-and-stick representation of aH adsorption/desorption reaction mediated through a H radical. (right) Monte Carlo estimates of the H coverage of the diamond surface at different temperatures based on quantum mechanically determined reaction barriers and reaction rates. |
Abstract
Hydrogen radical attacks and subsequent hydrogen migrations are considered to play an important role in the atomic-scale mechanisms of diamond chemical vapour deposition growth. We perform a comprehensive analysis of the reactions involving H-radical and vacancies on H-passivated diamond surfaces exposed to hydrogen radical-rich atmosphere. By means of first principles calculations—density functional theory and climbing image nudged elastic band method—transition states related to these mechanisms are identified and characterised. In addition, accurate reaction rates are computed using variational transition state theory. Together, these methods provide—for a broad range of temperatures and hydrogen radical concentrations—a picture of the relative likelihood of the migration or radical attack processes, along with a statistical description of the hydrogen coverage fraction of the (100) H-passivated surface, refining earlier results via a more thorough analysis of the processes at stake. Additionally, the migration of H-vacancy is shown to be anisotropic, and occurring preferentially across the dimer rows of the reconstructed surface. The approach used in this work can be generalised to other crystallographic orientations of diamond surfaces or other semiconductors.
Permanent link to this article: https://dannyvanpoucke.be/2024-paper-hadsorption-emerick-en/
Jan 10 2024
Cover Nature Reviews Physics
| Authors: | Emanuele Bosoni, Louis Beal, Marnik Bercx, Peter Blaha, Stefan Blügel, Jens Bröder, Martin Callsen, Stefaan Cottenier, Augustin Degomme, Vladimir Dikan, Kristjan Eimre, Espen Flage-Larsen, Marco Fornari, Alberto Garcia, Luigi Genovese, Matteo Giantomassi, Sebastiaan P. Huber, Henning Janssen, Georg Kastlunger, Matthias Krack, Georg Kresse, Thomas D. Kühne, Kurt Lejaeghere, Georg K. H. Madsen, Martijn Marsman, Nicola Marzari, Gregor Michalicek, Hossein Mirhosseini, Tiziano M. A. Müller, Guido Petretto, Chris J. Pickard, Samuel Poncé, Gian-Marco Rignanese, Oleg Rubel, Thomas Ruh, Michael Sluydts, Danny E.P. Vanpoucke, Sudarshan Vijay, Michael Wolloch, Daniel Wortmann, Aliaksandr V. Yakutovich, Jusong Yu, Austin Zadoks, Bonan Zhu, and Giovanni Pizzi |
| Journal: | Nature Reviews Physics 6(1), (2024) |
| doi: | web only |
| IF(2021): | 36.273 |
| export: | NA |
| pdf: | <NatRevPhys> |
Abstract
The cover of this issue shows an artistic representation of the equations of state of the periodic table elements, calculated using two all-electron codes in each of the 10 crystal structure configurations shown on the table. The cover image is based on the Perspective Article How to verify the precision of density-functional-theory implementations via reproducible and universal workflows by E. Bosoni et al., https://doi.org/10.1038/s42254-023-00655-3. (The related paper can be found here.)

Cover Nature Reviews Physics: Accuracy of DFT modeling in solids
Permanent link to this article: https://dannyvanpoucke.be/paper2024_accuracycover-en/
Dec 22 2023
Materiomics Chronicles: week 13 & 14
Weeks eleven and twelve gave some rest, needed for the last busy week of the semester: week 13. During this week, I have an extra cameo in the first year our materiomics program at UHasselt.

NightCafe’s response to the prompt: “Professor teaching quantum chemistry.”
Within the Bachelor of chemistry, the courses introduction to quantum chemistry and quantum and computational chemistry draw to a close, leaving just some last loose to tie up. For the second bachelor students in chemistry, this meant diving into the purely mathematical framework describing the quantum mechanical angular momentum and discovering spin operators are an example, though they do not represent an actual rotating object. Many commutators were calculated and ladder operators were introduced. The third bachelor students in chemistry dove deeper in the quantum chemical modeling of simple molecules, both in theory as well as in computation using a new set of jupyter notebooks during an exercise session.
In the first master materiomics, I had gave the students a short introduction into high-throughput modeling and computational screening approaches during a lecture and exercise class in the course Materials design and synthesis. The students came into contact with materials project via the web-interface and the python API. For the course on Density Functional Theory there was a final guest response lecture, while in the course Machine learning and artificial intelligence in modern materials science a guest lecture on optimal control was provided. During the last response lecture, final questions were addressed.
With week 14 coming to a close, the first semester draws to an end for me. We added another 15h of classes, ~1h of video lecture, and 3h of guest lectures, putting our semester total at 133h of live lectures (excluding guest lectures, obviously). January and February brings the exams for the second quarter and first semester courses.
I wish the students the best of luck with their exams, and I happily look back at surviving this semester.
Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-13-14/
Dec 13 2023
How to verify the precision of density-functional-theory implementations via reproducible and universal workflows
| Authors: | Emanuele Bosoni, Louis Beal, Marnik Bercx, Peter Blaha, Stefan Blügel, Jens Bröder, Martin Callsen, Stefaan Cottenier, Augustin Degomme, Vladimir Dikan, Kristjan Eimre, Espen Flage-Larsen, Marco Fornari, Alberto Garcia, Luigi Genovese, Matteo Giantomassi, Sebastiaan P. Huber, Henning Janssen, Georg Kastlunger, Matthias Krack, Georg Kresse, Thomas D. Kühne, Kurt Lejaeghere, Georg K. H. Madsen, Martijn Marsman, Nicola Marzari, Gregor Michalicek, Hossein Mirhosseini, Tiziano M. A. Müller, Guido Petretto, Chris J. Pickard, Samuel Poncé, Gian-Marco Rignanese, Oleg Rubel, Thomas Ruh, Michael Sluydts, Danny E.P. Vanpoucke, Sudarshan Vijay, Michael Wolloch, Daniel Wortmann, Aliaksandr V. Yakutovich, Jusong Yu, Austin Zadoks, Bonan Zhu, and Giovanni Pizzi |
| Journal: | Nature Reviews Physics 6(1), 45-58 (2024) |
| doi: | 10.1038/s42254-023-00655-3 |
| IF(2021): | 36.273 |
| export: | bibtex |
| pdf: | <NatRevPhys> <ArXiv:2305.17274> |
 |
| Graphical Abstract: “We hope our dataset will be a reference for the field for years to come,” says Giovanni Pizzi, leader of the Materials Software and Data Group at the Paul Scherrer Institute PSI, who led the study. (Image: Paul Scherrer Insitute / Giovanni Pizzi) |
Abstract
Density-functional theory methods and codes adopting periodic boundary conditions are extensively used in condensed matter physics and materials science research. In 2016, their precision (how well properties computed with different codes agree among each other) was systematically assessed on elemental crystals: a first crucial step to evaluate the reliability of such computations. In this Expert Recommendation, we discuss recommendations for verification studies aiming at further testing precision and transferability of density-functional-theory computational approaches and codes. We illustrate such recommendations using a greatly expanded protocol covering the whole periodic table from Z = 1 to 96 and characterizing 10 prototypical cubic compounds for each element: four unaries and six oxides, spanning a wide range of coordination numbers and oxidation states. The primary outcome is a reference dataset of 960 equations of state cross-checked between two all-electron codes, then used to verify and improve nine pseudopotential-based approaches. Finally, we discuss the extent to which the current results for total energies can be reused for different goals.
Permanent link to this article: https://dannyvanpoucke.be/paper-aiidaconsortium2023-en/
Dec 10 2023
Materiomics Chronicles: week 11 & 12
After the exam period in weeks nine and ten, the eleventh and twelfth week of the academic year bring the second quarter of our materiomics program at UHasselt for the first master students. Although I’m not coordinating any courses in this quarter, I do have some teaching duties, including being involved in two of the hands-on projects.
As in the past 10 weeks, the bachelor students in chemistry had lectures for the courses introduction to quantum chemistry and quantum and computational chemistry. For the second bachelor this meant they finally came into contact with the H atom, the first and only system that can be exactly solved using pen and paper quantum chemistry (anything beyond can only be solved given additional approximations.) During the exercise class we investigated the concept of aromatic stabilization in more detail in addition to the usual exercises with simple Schrödinger equations and wave functions. For the third bachelor, their travel into the world of computational chemistry continued, introducing post-Hartree-Fock methods with also include the missing correlation energy. This is the failure of Hartree-Fock theory, making it a nice framework, but of little practical use for any but the most trivial molecules (e.g. H2 for example already being out of scope). We also started looking into molecular systems, starting with simple diatomic molecules like H2+.
SnV split vacancy defect in diamond.
In the master materiomics, the course Machine learning and artificial intelligence in modern materials science hosted a guest lecture on Large Language Models, and their use in materials research as well as an exercise session during which the overarching ML study of the QM9 dataset was extended. During the course on Density Functional Theory there was a second lab, this time on conceptual DFT. For the first master students, the hands-on project kept them busy. One group combining AI and experiments, and a second group combining DFT modeling of SnV0 defects in diamond with their actual lab growth. It was interesting to see the enthusiasm of the students. With only some mild debugging, I was able to get them up and running relatively smoothly on the HPC. I am also truly grateful to our experimental colleagues of the diamond growth group, who bravely set up these experiments and having backup plans for the backup plans.
At the end of week 12, we added another 12h of classes, ~1h of video lecture, ~2h of HPC support for the handson project and 6h of guest lectures, putting our semester total at 118h of live lectures. Upwards and onward to weeks 13 & 14.
Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-11-12/
Nov 26 2023
Materiomics Chronicles: week 9 & 10
With the end of the first quarter in week eight, the nine and tenth week of the academic year were centered around the first batch of exams for the first master students of our materiomics program at UHasselt. For the other students in the second master and bachelor, academic life continued with classes.
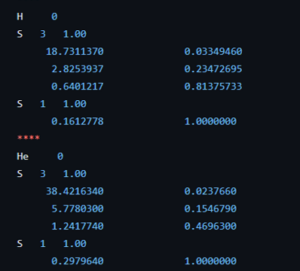
Coefficients of the 63-1G basis set for the H and He atom.
The course introduction to quantum chemistry starts to hone in on the first actual fully realistic system: the H atom. But before we get there, the students of the second bachelor chemistry extended their particle on a ring model system to an infinite number of ring systems: i.e. discs, spheres, and balls. Separation of variables has no longer any secrets for them. Now they are ready for reality after many weeks of abstract toy models. The third bachelor students on the other hand had their first ever contact with real practical quantum chemistry (i.e. computational chemistry) during the course quantum and computational chemistry. They learned about Hartree-Fock, the self-consistent field method, basis sets and slater orbitals. They entered this new world with a practical exercise class where, using jupyter notebooks and the psi4 package, they performed their first even quantum chemical calculations. Starting with the trivial H and He atom systems as a start, since for these we have calculated exact solutions during the classes of this course. This way, we learned about the quality of different basis sets and the time of calculations.
In the master materiomics, the first master students had their exams on Fundamentals of materials modeling, and Properties of functional materials, where all showed they understood the topics presented to sufficient degree making them ready for the second quarter. For the second master students, the course on Density Functional Theory held a lecture on the limitations of DFT and a guest lecture on conceptual DFT.
With week 10 drawing to a close, we added another 15h of classes, ~1h of video lecture and 2h of guest lectures, putting our semester total at 106h of live lectures. Upwards and onward to weeks 11 & 12.
Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-9-10/
Nov 12 2023
Materiomics Chronicles: week 8
After the complexities of week seven, week eight brings the last lecture week of the first quarter of the academic year. After this week, the students of our materiomics program at UHasselt will start studying for a first batch of exams. It also means with this week, their basic courses come to an end and they have all been brought up to speed and to a similar level, needed for the continuation of their study in the materiomics program.
In the bachelor program, the third bachelor chemistry students ended their detailed study of the He atom in the course quantum and computational chemistry with the investigation of its excited states. They learned about the splitting of in singlet and triplet states as well as Fermi-holes and heaps.
Vulcano-plot of small data model quality of model instances in a large ensemble. Taken from our paper “Small Data Materials Design with Machine Learning: When the Average Model Knows Best“, J. Appl. Phys. 128, 054901 (2020)
The first mater materiomics students got their last lecture in the course Fundamentals of materials modeling, where we looked into some examples of application of machine learning in materials research. We also brought all levels of the course together and imagined how to link these in a multiscale project. Starting from the example of a windmill we discussed the application of computational materials modeling at different scales. For the course Properties of functional materials, the third and final presentation and discussion was held, now focusing on characterization methods. The second master students had response lectures for the courses on Density Functional Theory and Machine learning and artificial intelligence in modern materials science where the various topics of the self study were discussed (e.g., concepts of Neural Networks in case of the latter).
At the end of this week, we have added another 8h of live lectures, putting our semester total at 99h of live lectures. With the workload of the first master materiomics coming to an end, the following chronicles will be biweekly. Upwards and onward to week 9&10.
Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-8/
Nov 05 2023
Materiomics Chronicles: week 7
After a relatively chill week six, the seventh week of the academic year ended up being complicated. As it was fall-break the week only consisted of two class days at university. However, primary schools are closed entirely so our son was at home having a holiday, while both parents were trying to juggle classes and project proposal deadlines as well as additional administrative reporting. A second evaluation meeting with the students of our materiomics program at UHasselt took place (second master this time), and also these students appreciated the effort put into creating their classes.
Although there were only two days of teaching, this did not mean there was little work there. The students of the second bachelor in chemistry extended their knowledge of a particle in a box to the model of a particle on a ring, during the course introduction to quantum chemistry. Similar as for a particle in a box, this can be considered a simplified model for a circular molecule like benzene, allowing us to estimate the first excitation quite accurately.
For the course Fundamentals of Materials Modeling, there was a lecture introducing the first master students materiomics into the very basics of machine learning, as well as an exercise session. During these, the students learned about linear regression, decision trees and support vector machines. This class was also open to students of the bachelor programs to get a bit of an idea of the content of the materiomics program. Finally, the first master students also presented the results of their lab on finite element modeling as part of the course Fundamentals of Materials Modeling. They presented flow studies around arrows, reef and car models, as well as heat transfer in complex partially insulated systems, as well as sinking boats. They showed they clearly gained insight through this type of hands-on tasks, which is always a joy to note, resulting in grades reflecting their efforts and insights.
Though this week was rather short, we added another 6h of classes, putting our semester total at 91h of live lectures. Upwards and onward to week 8.
Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-7/
Oct 29 2023
Materiomics Chronicles: week 6
After surviving week five, the sixth week of the academic year feels almost relaxing. However, all the effort is worth it, and I was happy to hear the students of our materiomics program at UHasselt appreciate the effort put into creating their classes, during an evaluation meeting.
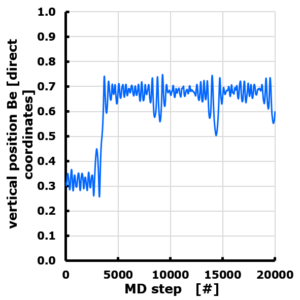
The evolution of the Z position of a Be atom on Graphene. Periodic cell with 10 Angstrom vacuum along z direction. Z position is given in direct coordinates (0…1), with the graphene sheet positioned at z=0 (=1). The Be atom is van der Waals bonded, and moves through the vacuum to attach to the “bottom” side of the sheet, though originally positioned at the “top” side.
Though the week was not as intense as the week before does not mean there were no classes at all. The second bachelor students in chemistry continued their studies of particles in simple potentials though the study of a particle in a square infinite potential well during the course introduction to quantum chemistry. During the course quantum and computational chemistry, the third bachelor chemistry, the He atom was now studied by means of the variational method, introducing the concepts of effective nuclear charge and shielding in a natural way.
While the bachelor students could take a backseat approach during the lectures (except for calculating some bbracket integrals), the master materiomics students had to do most of the heavy lifting during their classes. For the course on Density Functional Theory there was response lecture as well as a lab-session where they studied the dynamics of Be on and around graphene, while the first master students had their second presentation & discussion session on the computational aspects of the papers studied in the course Properties of functional materials.
At the end of this week, we added another 11h of live classes and ~2h of video lectures, putting our semester total at 85h of live lectures. Upwards and onward to week 7.
Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-6/