Category: blog

Jun 23 2025

MSc Materiomics defences & new QuATOMs members

MSc Thesis presentation of Brent Motmans and Eleonora Thomas (master materiomics students 2025). Both presenting applications of ML in materials research.

MSc Thesis presentation of Brent Motmans and Eleonora Thomas (master materiomics students 2025). Both presenting applications of ML in materials research: Machine Learning particle sizes using small lab-scale datasets (Brent) and development of Machine Learned Interatomic Potentials for the modelling of (the dynamics of) H-based defects in diamond.

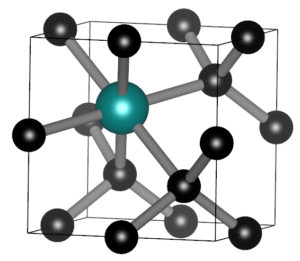
Today we had the MSc presentations of the master Materiomics. The culmination of two year of hard study and intens research activities resulting in a final master thesis paper. This year the QuATOMs group hosted two MSc students: Brent Motmans and Eleonora Thomas. Brent Motmans performed his research in a collaboration between the QuATOMs and DESINe groups, and investigated the application of small data machine learning for the prediction of the particle size of Cu nanoparticles. His study shows that even with a dataset of less than 20 samples a reasonable 6 feature model can be created. As in previous research, he found that standard hyperparameter tuning fails, but human intervention can resolve this issue. Eleonora Thomas on the other hand introduced Machine Learned Interatomic Potentials (MLIPs) into the group. By investigating different in literature available MLIPs, she pinpointed strengths and weaknesses of the different models, as well as the technical needs for persuing such research further in our group. As collatoral, she was able to generate a model for H diffusion in diamond, with an MAE for the total energy of <10meV/atom, competing with models like google deep-mind’s GNoME.

While working on their MSc thesis, Brent and Eleonora also applied for fellowship funding for a PhD position, and we are happy to announce both Brent and Eleonora won their grant, and will be starting in the QuATOMs group as new PhD students comming academic year. Eleonora Thomas will be working on the modelling of Lignin solvation, while Brent will work in a collaboration with  the HyMAD group on the modeling of hybrid perovskites.

Permanent link to this article: https://dannyvanpoucke.be/msc-materiomics-defences-new-quatoms-members/

Jan 21 2025

Machine Learning and Artificial Intelligence in modern materials science

  • Filed under blog

  • January 21, 2025

One of the most joyful parts of teaching, is when you read a student paper and see their joy of the research shine through.

This year was the second year I taught the course “Machine Learning and Artificial Intelligence in modern materials science“, an elective course in the second master materiomics program. As with my other computational courses, there is a strong hands-on component present in this course: a semester long homework assignment, culminating in a paper and presentation of the work done. The basic idea behind the assignment is simple: Take the QM9 dataset and study it using machine learning and artificial intelligence, incorporating things you learn during the course. In practice this means a lot of coding with for example scikit-learn in combination with using every ounce of physical and chemical intuition they gathered during their previous courses. The absolute freedom generally results in some initial trepidation, but intermediate feedback and the growing understanding that the journey is the the actual goal results in some amazing work.

At the end of the semester, I had three papers before me, which could only be written by these three students (Materiomics is a new program, so having 3 of the 7 students picking a rather hard core computational course is good 😉 ). You could feel their own backgrounds and interests seeping through, as well as the fun they had doing so. There was the engineer who approached the problem from a pipeline perspective, the chemist comparing the efficacy of various fingerprints as features, and the physicist who build a new small fingerprint from scratch creating a linear regression model that outperformed all else having R² =1. The last one is a very nice example of frugal computing, of which we do need more in a world suffering climate change. It was also interesting to see also how three totally different stories also hint at the same underlying properties of the dataset (same target being the hardest to predict), a consistency which provides a level of meta-validation of the results. The students themselves also learned to be critical of their own work by comparing the results of different methods used to attack their own research question.

At the end of this course, it is clear they learned more about artificial intelligence than what is possible by just reading about it. The understood the entire workflow of which training is merely a small part, they learned directly the importance of having good quality data and features, and most importantly they learned that they themselves need to be the I in AI, to be successful…and finally, maybe us four should put our heads together and combine this work into a real research paper, as to celebrate the great research done as a “mere homework-assignment”.

Permanent link to this article: https://dannyvanpoucke.be/machine-learning-and-artificial-intelligence-in-modern-materials-science/

Jan 01 2025

Review of 2024

  • Filed under blog

  • January 1, 2025

Happy 2025

2023 and 2024 have been an intense ride, with both the materiomics program, the tenure track and the research group. Since the previous overview in 2022, the QuATOMs group has seen some growth with the arrival of three new members (Pauline Castenetto, Thijs van Wijk, and Aylin Melan). In addition, Emerick Guillaume defended his PhD on the study of diamond growth.

These are not the only things which happened the last two years, so let us look back at 2023 and 2024 one last time, keeping up with  tradition.

1. Publications: +4 (and currently a handful in progress)

2. Cover publication: +1

Cover Nature Reviews Physics: Accuracy of DFT

3. Project proposals accepted: +2

  • QuantumLignin: Elucidating the interactions of lignin building blocks with their environment for the creation of additive models by means of quantum mechanical modelling.
  • AI-accelerated quantum mechanical modelling of the optical properties of semiconductor materials: from colour centres in diamond to transition-metal oxides.

4. Completed refereeing tasks: +20

  • ACS Photon
  • Journal of Physics D: Applied Physics (2x)
  • Philosophical Transactions (2x)
  • Journal of Materials Chemistry A (2x)
  • Journal of Physical Chemistry (3x)
  • Diamond and Related Materials (11x)

5. Conferences & seminars: +7/+1 (Attended & Organised)

  • SBDD XXVII & SBDD XXVIII, Hasselt University, Belgium, March 15th-17th, 2023 & February 28th-March 1st, 2024 [poster presentations, PhD students & MSc student]
  • EAB-workshop on AI in Higher Education, UHasselt, Belgium, April 24th, 2024 [oral presentation]
  • DFT-2024: 20th International Conference on Density Functional Theory and its Applications, Paris, France, August 25th-30th, 2024 [oral presentation]
  • E-MRS Spring meeting 2023 & 2024, Strassbourg, France, May 29th-June 2nd, 2023 & May 27th-31st, 2024 [oral presentations]
  • Summer School: “Materiomics: Innovative Materials From Healthcare Across Quantum To Sustainable Technologies”, UHasselt, Belgium, September 4th-6th, 2024 [member of Organizating Committee; seminar]
  • NISM seminar: “Extreme Machine Learning – When the average model knows best”  (Prof. L. Henrard), UNamur, Belgium, September 12th, 2024 [invited seminar]

6. Supervised students:

  • BSc Projects Physics: 4
  • MSc Projects Materiomics: 3
  • Internships: 2

7. Hive-STM program:

And now, upward and onward, a new year, a fresh start.

Permanent link to this article: https://dannyvanpoucke.be/review-of-2024/

Sep 22 2024

End of summer, and the start of a new academic year.

  • Filed under blog

  • September 22, 2024

Mid September in Hasselt means the start of a new academic year. It brings to an end a summer of doing some unrestricted research. Especially the last month has been extremely busy.

  • The DFT2024 conference in Paris from August 25th until 30th, where I presented our recent work on the GeV defect, which we will be submitting shortly.
  • The materiomics summer school, where I gave a lecture on performing practical quantum mechanical calculations,
  • The public PhD defense of Emerick Guillaume (QuATOMs group member) on the growth of diamond: congratulations Emerick!
  • A seminar at UNamur on “extreme machine learning”, discussing our work on small datasets and some of the work I did this summer on a spray coating dataset.

Today the first week of academic year ended, and I already had the pleasure teaching quantum mechanics and modelling courses to chemistry and materiomics students. We also welcome 2 MSc materiomics students to the group: Brent Motmans and Eleonora Thomas. Brent will be working on an experimental-theoretical project, where the theoretical side will focus on machine learning of his experimental data. Eleonora on the other hand will be combining DFT and machine learning in her study of diamond. A very warm welcome to the QuATOMs group for both.

 

Permanent link to this article: https://dannyvanpoucke.be/end-of-summer-and-the-start-of-a-new-academic-year/

Sep 01 2024

New QuATOMs group member

During the last year, Esin Aylin Melan worked hard at her MSc Thesis within the QuATOMs group. Her research focus was centered on the impact of strain on the zero-phonon-line of the GeV color center in diamond. This work she presented, together with Thijs van Wijk, at the SBDD conference in Hasselt, and was presented as well at both the BPS and EMRS spring meeting of 2024. Before the summer she gave her (very good and enthusiastic) final presentation of the MSc thesis results, bringing her first real research project to good end. (Paper will follow later 🙂 )

Recently, she also received the great news that she was awarded a bilateral PhD Scholarship between UHasselt & UNamur. So from September first, she has started working on the modeling of color centers in diamond and oxides for the coming four years. Welcome to the QuATOMs team, and congratulations on the scholarship. We look forward to the enthusiasm and insights you’ll bring to the team.

Permanent link to this article: https://dannyvanpoucke.be/new-quatoms-group-member/

Jan 10 2024

Cover Nature Reviews Physics

Authors: Emanuele Bosoni, Louis Beal, Marnik Bercx, Peter Blaha, Stefan Blügel, Jens Bröder, Martin Callsen, Stefaan Cottenier, Augustin Degomme, Vladimir Dikan, Kristjan Eimre, Espen Flage-Larsen, Marco Fornari, Alberto Garcia, Luigi Genovese, Matteo Giantomassi, Sebastiaan P. Huber, Henning Janssen, Georg Kastlunger, Matthias Krack, Georg Kresse, Thomas D. Kühne, Kurt Lejaeghere, Georg K. H. Madsen, Martijn Marsman, Nicola Marzari, Gregor Michalicek, Hossein Mirhosseini, Tiziano M. A. Müller, Guido Petretto, Chris J. Pickard, Samuel Poncé, Gian-Marco Rignanese, Oleg Rubel, Thomas Ruh, Michael Sluydts, Danny E.P. Vanpoucke, Sudarshan Vijay, Michael Wolloch, Daniel Wortmann, Aliaksandr V. Yakutovich, Jusong Yu, Austin Zadoks, Bonan Zhu, and Giovanni Pizzi
Journal: Nature Reviews Physics 6(1), (2024)
doi: web only
IF(2021): 36.273
export: NA
pdf: <NatRevPhys>

Abstract

The cover of this issue shows an artistic representation of the equations of state of the periodic table elements, calculated using two all-electron codes in each of the 10 crystal structure configurations shown on the table. The cover image is based on the Perspective Article How to verify the precision of density-functional-theory implementations via reproducible and universal workflows by E. Bosoni et al., https://doi.org/10.1038/s42254-023-00655-3.  (The related paper can be found here.)

Cover Nature Reviews Physics: Accuracy of DFT modeling in solids

 

Permanent link to this article: https://dannyvanpoucke.be/paper2024_accuracycover-en/

Dec 22 2023

Materiomics Chronicles: week 13 & 14

Weeks eleven and twelve gave some rest, needed for the last busy week of the semester: week 13. During this week, I have an extra cameo in the first year our materiomics program at UHasselt.

NightCafe's response to the prompt: "Professor teaching quantum chemistry."

NightCafe’s response to the prompt: “Professor teaching quantum chemistry.”

Within the Bachelor of chemistry, the courses introduction to quantum chemistry and quantum and computational chemistry draw to a close, leaving just some last loose to tie up. For the second bachelor students in chemistry, this meant diving into the purely mathematical framework describing the quantum mechanical angular momentum and discovering spin operators are an example, though they do not represent an actual rotating object. Many commutators were calculated and ladder operators were introduced. The third bachelor students in chemistry dove deeper in the quantum chemical modeling of simple molecules, both in theory as well as in computation using a new set of jupyter notebooks during an exercise session.

In the first master materiomics, I had gave the students a short introduction into high-throughput modeling and computational screening approaches during a lecture and exercise class in the course Materials design and synthesis. The students came into contact with materials project via the web-interface and the python API. For the course on Density Functional Theory there was a final guest response lecture, while in the course Machine learning and artificial intelligence in modern materials science a guest lecture on optimal control was provided. During the last response lecture, final questions were addressed.

With week 14 coming to a close, the first semester draws to an end for me. We added another 15h of classes, ~1h of video lecture, and 3h of guest lectures, putting our semester total at 133h of live lectures (excluding guest lectures, obviously). January and February brings the exams for the second quarter and first semester courses.

I wish the students the best of luck with their exams, and I happily look back at surviving this semester.

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-13-14/

Dec 10 2023

Materiomics Chronicles: week 11 & 12

After the exam period in weeks nine and ten, the eleventh and twelfth week of the academic year bring the second quarter of our materiomics program at UHasselt for the first master students. Although I’m not coordinating any courses in this quarter, I do have some teaching duties, including being involved in two of the hands-on projects.

As in the past 10 weeks, the bachelor students in chemistry had lectures for the courses introduction to quantum chemistry and quantum and computational chemistry. For the second bachelor this meant they finally came into contact with the H atom, the first and only system that can be exactly solved using pen and paper quantum chemistry (anything beyond can only be solved given additional approximations.) During the exercise class we investigated the concept of aromatic stabilization in more detail in addition to the usual exercises with simple Schrödinger  equations and wave functions. For the third bachelor, their travel into the world of computational chemistry continued, introducing post-Hartree-Fock methods with also include the missing correlation energy. This is the failure of Hartree-Fock theory, making it a nice framework, but of little practical use for any but the most trivial molecules (e.g. H2 for example already being out of scope). We also started looking into molecular systems, starting with simple diatomic molecules like H2+.

SnV split vacancy defect in diamond.

SnV split vacancy defect in diamond.

In the master materiomics, the course Machine learning and artificial intelligence in modern materials science hosted a guest lecture on Large Language Models, and their use in materials research as well as an exercise session during which the overarching ML study of the QM9 dataset was extended. During the course on  Density Functional Theory there was a second lab, this time on conceptual DFT. For the first master students, the hands-on project kept them busy. One group combining AI and experiments, and a second group combining DFT modeling of SnV0 defects in diamond with their actual lab growth. It was interesting to see the enthusiasm of the students. With only some mild debugging, I was able to get them up and running relatively smoothly on the HPC. I am also truly grateful to our experimental colleagues of the diamond growth group, who bravely set up these experiments and having backup plans for the backup plans.

At the end of week 12, we added another 12h of classes, ~1h of video lecture, ~2h of HPC support for the handson project and 6h of guest lectures, putting our semester total at 118h of live lectures. Upwards and onward to weeks 13 & 14.

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-11-12/

Nov 26 2023

Materiomics Chronicles: week 9 & 10

With the end of the first quarter in week eight, the nine and tenth week of the academic year were centered around the first batch of exams for the first master students of our materiomics program at UHasselt. For the other students in the second master and bachelor, academic life continued with classes.

Coefficients of the 63-1G basis set for the H and He atom.

Coefficients of the 63-1G basis set for the H and He atom.

The course introduction to quantum chemistry starts to hone in on the first actual fully realistic system: the H atom. But before we get there, the students of the second bachelor chemistry extended their particle on a ring model system to an infinite number of ring systems: i.e. discs, spheres, and balls. Separation of variables has no longer any secrets for them. Now they are ready for reality after many weeks of abstract toy models. The third bachelor students on the other hand had their first ever contact with real practical quantum chemistry (i.e. computational chemistry) during the course quantum and computational chemistry. They learned about Hartree-Fock, the self-consistent field method, basis sets and slater orbitals. They entered this new world with a practical exercise class where, using jupyter notebooks and the psi4 package, they performed their first even quantum chemical calculations. Starting with the trivial H and He atom systems as a start, since for these we have calculated exact solutions during the classes of this course. This way, we learned about the quality of different basis sets and the time of calculations.

In the master materiomics, the first master students had their exams on Fundamentals of materials modeling, and Properties of functional materials, where all showed they understood the topics presented to sufficient degree making them ready for the second quarter. For the second master students, the course on Density Functional Theory held a lecture on the limitations of DFT and a guest lecture on conceptual DFT.

With week 10 drawing to a close, we added another 15h of classes, ~1h of video lecture and 2h of guest lectures, putting our semester total at 106h of live lectures. Upwards and onward to weeks 11 & 12.

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-9-10/

Nov 12 2023

Materiomics Chronicles: week 8

After the complexities of week seven, week eight brings the last lecture week of the first quarter of the academic year. After this week, the students of our materiomics program at UHasselt will start studying for a first batch of exams. It also means with this week, their basic courses come to an end and they have all been brought up to speed and to a similar level, needed for the continuation of their study in the materiomics program.

In the bachelor program, the third bachelor chemistry students ended their detailed study of the He atom in the course quantum and computational chemistry with the investigation of its excited states. They learned about the splitting of in singlet and triplet states as well as Fermi-holes and heaps.

Vulcanoplot

Vulcano-plot of small data model quality of model instances in a large ensemble. Taken from our paper “Small Data Materials Design with Machine Learning: When the Average Model Knows Best“, J. Appl. Phys. 128, 054901 (2020)

The first mater materiomics students got their last lecture in the course Fundamentals of materials modeling, where we looked into some examples of application of machine learning in materials research. We also brought all levels of the course together and imagined how to link these in a multiscale project. Starting from the example of a windmill we discussed the application of computational materials modeling at different scales. For the course Properties of functional materials, the third and final presentation and discussion was held, now focusing on characterization methods. The second master students had response lectures for the courses on Density Functional Theory and Machine learning and artificial intelligence in modern materials science where the various topics of the self study were discussed (e.g., concepts of Neural Networks in case of the latter).

At the end of this week, we have added another 8h of live lectures, putting our semester total at 99h of live lectures. With the workload of the first master materiomics coming to an end, the following chronicles will be biweekly. Upwards and onward to week 9&10.

 

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-8/