In the previous tutorial of the wordle-mania-series, we had a quick overview of how to construct a basic class in Python. Here we take our class adventure a step further and implement a child class. As before, the full source of this project can be found in our GitHub repo.
1. Building a child class.
The construction of a child class is near identical to the construction of a non-child class. The only difference being we need to somehow indicate the class is derived from another class. During our previous tutorial, we created the WordleAssistant class, so let’s use it as a parent for the WordleAssistant2 child class.
from .WordleAssistant import WordleAssistant class WordleAssistant2(WordleAssistant): pass
First, note that we need to import the WordleAssistant class, which is stored in a file WordleAssistant.py, contained in the same folder as the file containing our child class (hence the “.” in front of WordleAssistant). At this point, most python developers will hate me for using the same name for what is considered a module and a class, as you could put multiple classes in a single file. Then again, once you start writing object oriented code, it is good practice to put only one class in a single file, which makes it rather strange to use different names.
Second, we put parent class between the brackets of the child class. Through this simple action, and the magic of inheritance, we just created an entirely new class containing all functions and functionality of the parent class. The keyword pass is used to indicate no further methods and attributes will be added.
2. Child class individuality.
Of course, we want our child class to not be just a wrapper of the parent class. The choice to use a child class can be twofold:
-
- Extension of an existing class. This can either be because you are not the developer of the parent class, or (in case you are the developer) because you don’t want to accidentally destroy a working piece of software (c.q. parent class) while trying out some new features, or …
- Modification/implementation of specific class behavior. The standard (trivial) examples involve drawing classes, which in one child class draw circles, while in another it draws squares.
- Both of the above.
In our case, we are going to ‘upgrade‘ our WordleAssistant class by considering the prevalence of every letter at the specific position in the 5-letter word. This in contrast to our original implementation which only considered the prevalence of a letter anywhere in the word. Adding new functionality with “new” methods and attributes, happens as for the parent class. You just define the new methods and attributes, which should have names that differ from the names for methods and attributes already used by the parent class.
However, sometimes, you may want or have to modify existing methods. You can either replace the entire functionality overwriting that of the parent method, or you may extend that functionality.
2.1. Extending methods.
When you still want to make use of the functionality of the method of the parent class you could just copy that code, and add your own code to extend it. This however makes your code hard to maintain, as each time the parent class code is modified, you would need to modify your child class as well. This increases the risk of breaking the code. Luckily, similar as programming languages like C++ and Object Pascal, there is a useful trick which allows you to wrap the parent class code in your overwritten child class method. A location where this trick is most often used is the initialization method. Below you can see the __init__ function of the WordleAssistant2 child class.
def __init__(self, size: int = 5, dictionary : str = None ): super().__init__(size, dictionary) self.FullLettPrevSite = self._letterDistSite(self.FullWorddict) self.CurLettPrevSite = copy.deepcopy(self.FullLettPrevSite)
The super() function indicates we are going to access the methods of the parent of the class we are working in at the moment. The super().__init__() method therefor refers to the __init__ method of the WordleAssistant class. This means the __init__ method of the WordleAssistant2 child class will first perform the __init__ method of the WordleAssistant class and then execute the following two statements which initialize our new attributes. Pretty simple, and very efficient.
2.2. Overwriting methods.
In some cases, you don’t want to retain anything of the parent method. By overwriting a method, your child class will now use a totally new code which does not retain any functionality of the parent method. Note that in the previous section we were also overwriting the __init__ method, but we retained some functionality via the call using super(). An example case of a full overwrite is found in the _calcScore method:
def _calcScore(self, WD: dict, LP: list): for key in WD: WD[key]['score'] = 0 for i in range(self.WordleSize): WD[key]['score'] += self.CurLettPrevSite[i][WD[key]['letters'][i]]
Although this method can still make use of attributes (self.WordleSize) and methods of the parent class, the implementation is very different and unrelated to that of the parent class. This is especially true in case of the python scripting language. Where a programming language like C++ or Object Pascal will require you to return the same type of result (e.g. the parent class returns an integer, then the child class can not return a string, or even a float.), python does not care. It places the burden of checking this downstream: i.e. with the user. As a developer, it is therefore good practice to be better than standard python and take away as much of this burden from the future users of your code (which could be your future self.)
Finally, a small word of caution with regard to name mangling. Methods with two leading underscores can not be overwritten in the child class in the sense that these methods are not accessible outside the parent class. This means also inside a child class these methods are out of scope. If we had a __calcScore method instead, creating an additional __calcScore in our child class would give rise to a lot of confusion (for python and yourself) and unexpected behavior.


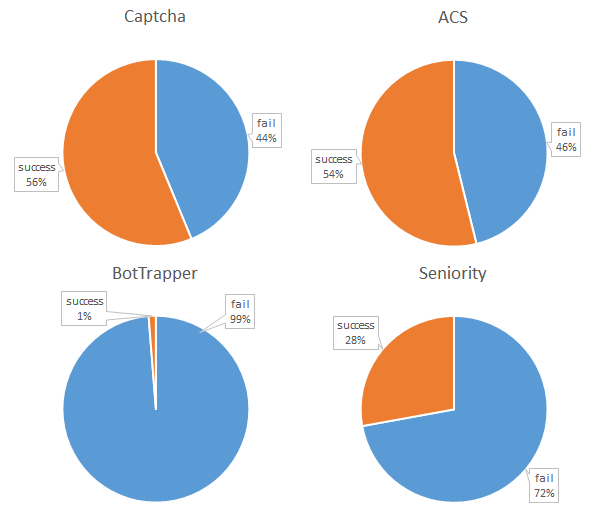
 What started out with the intention of being an almost trivial exercise in building a web-form, turned into a steep learning curve about web-development and cyber-security. I am aware there exists many tools which generate forms for websites or even provide you a platform which hosts the form (e.g.,
What started out with the intention of being an almost trivial exercise in building a web-form, turned into a steep learning curve about web-development and cyber-security. I am aware there exists many tools which generate forms for websites or even provide you a platform which hosts the form (e.g., 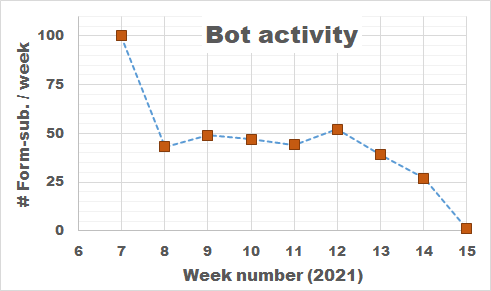

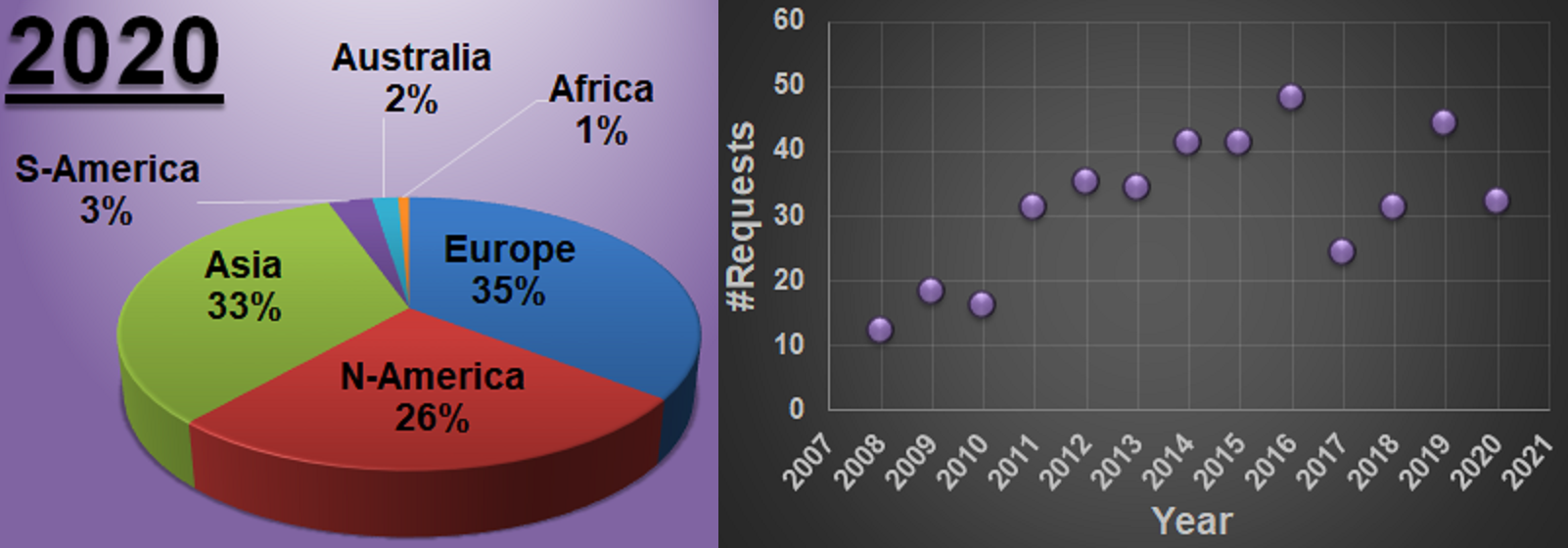



 A new year, a new beginning.
A new year, a new beginning.