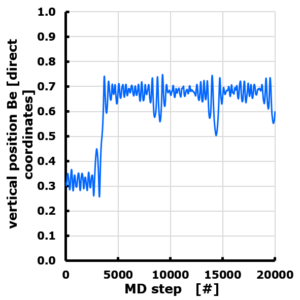
Weeks eleven and twelve gave some rest, needed for the last busy week of the semester: week 13. During this week, I have an extra cameo in the first year our materiomics program at UHasselt.

NightCafe’s response to the prompt: “Professor teaching quantum chemistry.”
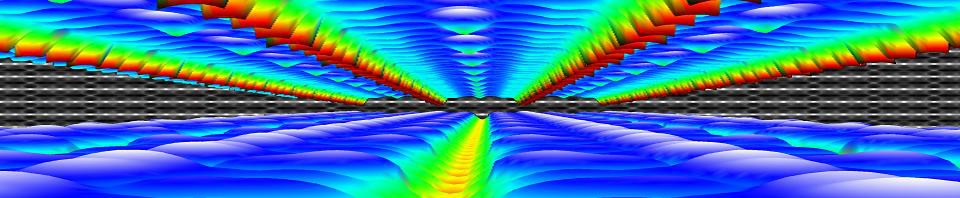
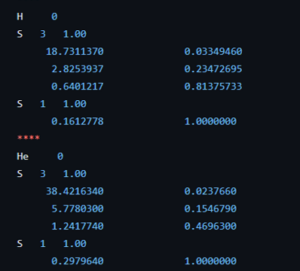
Within the Bachelor of chemistry, the courses introduction to quantum chemistry and quantum and computational chemistry draw to a close, leaving just some last loose to tie up. For the second bachelor students in chemistry, this meant diving into the purely mathematical framework describing the quantum mechanical angular momentum and discovering spin operators are an example, though they do not represent an actual rotating object. Many commutators were calculated and ladder operators were introduced. The third bachelor students in chemistry dove deeper in the quantum chemical modeling of simple molecules, both in theory as well as in computation using a new set of jupyter notebooks during an exercise session.
In the first master materiomics, I had gave the students a short introduction into high-throughput modeling and computational screening approaches during a lecture and exercise class in the course Materials design and synthesis. The students came into contact with materials project via the web-interface and the python API. For the course on Density Functional Theory there was a final guest response lecture, while in the course Machine learning and artificial intelligence in modern materials science a guest lecture on optimal control was provided. During the last response lecture, final questions were addressed.
With week 14 coming to a close, the first semester draws to an end for me. We added another 15h of classes, ~1h of video lecture, and 3h of guest lectures, putting our semester total at 133h of live lectures (excluding guest lectures, obviously). January and February brings the exams for the second quarter and first semester courses.
I wish the students the best of luck with their exams, and I happily look back at surviving this semester.