Oct 22 2023

Materiomics Chronicles: week 5

After week four, this fifth week of the academic year is most arguably the most intense and hectic week of teaching. With 22h of classes and still two classes that needed to be prepared from scratch (even including weekends time was running out), I’m tired but happy it is over. However, all the effort is worth it, and I was happy to hear the students of our materiomics program at UHasselt appreciate the effort put into creating their classes, during an evaluation meeting.

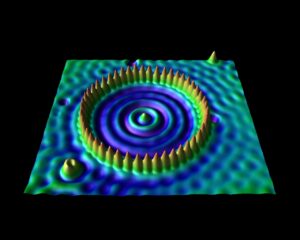
The corral is an artificial structure created from 48 iron atoms (the sharp peaks) on a copper surface. The wave patterns in this scanning tunneling microscope image are formed by copper electrons confined by the iron atoms. Don Eigler and colleagues created this structure in 1993 by using the tip of a low-temperature scanning tunneling microscope (STM) to position iron atoms on a copper surface, creating an electron-trapping barrier. This was the first successful attempt at manipulating individual atoms and led to the development of new techniques for nanoscale construction.source: https://www.nisenet.org/catalog/scientific-image-quantum-corral-top-view

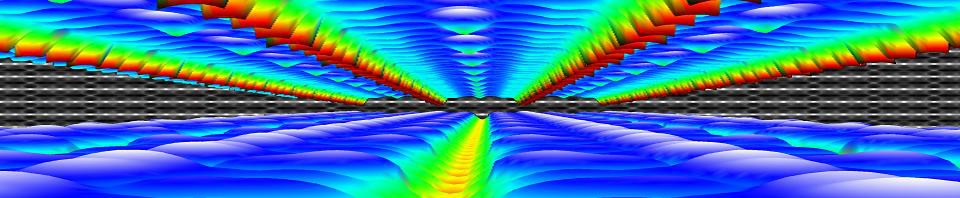
The corral is an artificial structure created from 48 iron atoms (the sharp peaks) on a copper surface. The wave patterns in this scanning tunneling microscope image are formed by copper electrons confined by the iron atoms. Don Eigler and colleagues created this structure in 1993 by using the tip of a low-temperature scanning tunneling microscope (STM) to position iron atoms on a copper surface, creating an electron-trapping barrier. This was the first successful attempt at manipulating individual atoms and led to the development of new techniques for nanoscale construction.
source: https://www.nisenet.org/catalog/scientific-image-quantum-corral-top-view

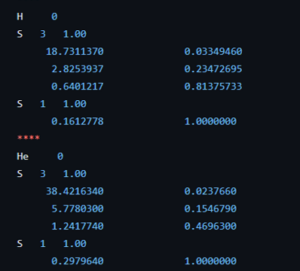
For the second bachelor students in chemistry the introduction to quantum chemistry finally put them into contact with some “real” quantum mechanics when they were introduced into the world of potential barriers, steps, and wells. Though these are still abstract and toy-model in nature, they provide a first connection with reality, where they can be seen as crude approximations of the potential experienced by valence electrons near the surface, or STM experiments. They were also introduced to my favorite quantum system related to this course: the quantum corral. Without any effort it can be used in half a dozen situations with varying complexity to show and learn basic quantum mechanics. For the third bachelor chemistry students the course quantum and computational chemistry finally provided them the long promised first example of a non-trivial quantum chemical object: The Helium atom. With it’s two electrons, we break free of the H-atom(-like)  world. Using perturbation theory and Slater determinant wave functions, we made our first approximations of its energy. In addition, these students also had a seminar for their course Introductory lectures in preparation to the bachelor project (Kennismakingstraject m.b.t. stage en eindproject, in Dutch). During this lecture I gave a brief introduction and overview of the work I did in the past and the work we do in our research group QuATOMs, which although “quantum” is quite different of what the students experience during their courses on quantum chemistry.

In the materiomics program, the first master students continued their travels into the basics of force-fields during the lecture of the course Fundamentals of materials modelling. The exercise class of this week upped the ante by moving from ASE to LAMMPS for practical modeling of alkane chains, which was also the topic of their second lab session. In the course Properties of functional materials, we investigated the ab initio modelling of vibrations. During the exercise classes we investigated precalculated phonon spectra in the materials-project database, as well as calculated our own vibrational spectrum at the gamma-point of the first Brillouin zone. During the second master course Machine learning and artificial intelligence in modern materials science the central theme was GIGO (Garbage-In-Garbage-Out). How can we make sure our data is suitable and good enough for our models to return useful results. We therefore looked into data-preparation & cleaning, as well as  clustering methods.

At the end of this week, we have added another 22h of live lectures and ~1h of video lectures, putting our semester total at 74h of live lectures. Upwards and onward to week 6.

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-5/

Oct 15 2023

Materiomics Chronicles: week 4

Week four of the academic year at the chemistry and materiomics programs of UHasselt, we are stepping up the pace a bit…at least for me. The students continue to dive deeper into the various subjects furthering their knowledge gained in the previous weeks.

In the bachelor chemistry program, the third bachelor chemistry extended their knowledge of variational theory to excited states, in the course quantum and computational chemistry. They also saw some first glimpses of the mathematical setup which makes the use of computational methods so important and powerful in quantum chemistry.  Finally they proved the Hellmann-Feynman Theorem which makes structure optimization in quantum chemistry practically feasible. For the second bachelor chemistry, the course introduction to quantum chemistry was focused on the time-dependent Schrödinger equation and the uncertainty principle.

In the first master materiomics, I was the  main player this week (and will also be so next week) teaching the classes of two of the three courses. In the course Properties of functional materials, the second module started, which is centered on the computational (quantum mechanical) modeling of materials properties. Here the students build on their recently acquired expertise in DFT to gain further insights into electronic structure calculations both in theory and in practice. In addition, the students also had their first seminar presentation where they present their understanding after studying two papers within the context of the concepts presented during the first module of the course. In the course Fundamentals of materials modelling, we moved to a new level of modeling: atomistic modeling using force-fields. The freshly gained knowledge was also here directly applied through the modeling of bulk aluminum using the ASE library in a jupyter notebook. (For many a first contact with python.) Finally, the students of the second master learned about “dynamical” modeling, in the course on Density Functional Theory, covering NEB calculations for energy barriers as well as basic molecular dynamics (with examples such as the water molecule below).

 

At the end of this week, we have added another 17h of live lectures and ~1h of video lectures, putting our semester total at 52h of live lectures. Upwards and onward to week 5.

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-4/

Oct 07 2023

Materiomics Chronicles: week 3

In week three of the academic year at the chemistry and materiomics programs of UHasselt, the students started to put their freshly gained new knowledge of weeks 1 and 2 into practice with a number of exercise classes.

For the second bachelor chemistry students, this meant performing their first calculations within the context of the course introduction to quantum chemistry. At this point this is still very mathematical (e.g., calculating commutators) and abstract (e.g., normalizing a wave function or calculating the probability of finding a particle, given a simple wave function), but this will change, and chemical/physical meaning will slowly be introduced into the mathematical formalism. For the third bachelor chemistry, the course quantum and computational chemistry continued with perturbation theory, and we started with the variational method as well. The latter was introduced through the example of the H atom, for which the exact variational ground state was recovered starting from a well chosen trial wave function.

Infinite polymethylene glycol (POM) chain.

Ball-and-stick representation of an infinite polymethylene glycol (POM) chain.

In the master materiomics, the first master course fundamentals of materials modelling, dove into the details underpinning DFT introducing concepts like pseudo-potentials, the frozen-core approximation, periodic boundary conditions etc. This knowledge was then put into practice during a second exercise session working on the supercomputer, as a last preparation for the practical lab exercise the following day. During this lab, the students used the supercomputer to calculate the Young modulus of two infinite linear polymers. An intense practical session which they all executed with great courage (remember 2 weeks ago they never heard of DFT, nor had they accessed a supercomputer). Their report for this practical will be part of their grade.

For the second master materiomics, the course focused on Density Functional Theory consisted of a discussion lecture, covering the topics the students studied during their self study assignments. In addition, I recorded two video lectures for the blended learning part of the course. For the course Machine learning and artificial intelligence in modern materials science self study topics were covered in such a discussion lecture as well. In addition, the QM9 data set was investigated during an exercise session, as preparation for further detailed study.

At the end of this week, we have added another 16h of live lectures and ~1h of video lectures, putting our semester total at 35h of live lectures. Upwards and onward to week 4.

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-3/

Sep 30 2023

Materiomics Chronicles: week 2

After the more gentle introductions last week during the first lectures at UHasselt, this week we dove into the deep end.

For the students of the second bachelor chemistry  the course introduction to quantum chemistry dove into the postulates of quantum chemistry. They learned about the wave-function and operators, had their first contact with the mystics notation of quantum chemistry: the bra-ket notation. For the third bachelor chemistry, the course quantum and computational chemistry was centered around perturbation theory. In addition to the theory, we applied the method to the simple system of the infinite square potential.

The electron density in the primitive diamond unit cell.

In the master materiomics the course fundamentals of materials modeling was kicked into high gear, not only did the students learn the theory behind quantum mechanical modelling, they also had their fist experience on the supercomputers of the VSC. So in addition to the road from the standard Schrödinger equation to the Hohenberg-Kohn-Sham equations of DFT, they also traveled their first steps along the road from their somewhat familiar windows OS to the bash command-line environment of the HPC unix system.

Finally, as the course introduction into quantum chemistry is part of the preparatory program of the master materiomics, I started creating the narrated versions of those lectures as well (2h worth recording, corresponding to 4h of live lectures). As the available time is limited, we are going for single shot recordings which makes things exciting in that department as well.

At the end of this week, we have added another 7h of live lectures and 2h of video lectures, putting our semester total at 19h of lectures. Upwards and onward to week 3.

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-2/

Sep 24 2023

Materiomics Chronicles: week 1

The first week of the academic year at UHasselt has come to an end, while colleagues at UGent and KULeuven are still preparing for the start of their academic year next week. Good luck to all of you.

This week started full throttle for me, with classes for each of my six courses. After introductions in classes with new students (for me) in the second bachelor chemistry and first master materiomics, and a general overview in the different courses, we quickly dove into the subject at hand.

The second bachelor students (introduction to quantum chemistry) got a soft introduction into (some of) the historical events leading up to the birth of quantum mechanics such as the black body radiation, the atomic model and the nature of light. They encountered the duck-rabbit of particle-wave duality and awakened their basic math skills with the standing wave problem. For the third bachelor students, the course on quantum and computational chemistry started with a quick recap of the course introduction to quantum mechanics, making sure they are all again up to speed with concepts like braket-notation and commutator relations.

For the master materiomics it was also a busy week. We kicked of the 1st Ma course Fundamentals of materials modeling, which starts of calm and easy with a general picture of the role of computational research as third research paradigm. We discussed in which fields computational research can be found (flabbergasting students with an example in Theology: a collaboration between Sylvia Wenmackers & Helen De Cruz),  approximation vs idealization, examples of materials research at different scales, etc. As a homework assignment the students were introduced into the world of algorithms through the lecture of Hannah Fry (Should computers run the world). For the  2nd Ma, the courses on Density Functional Theory and Machine learning and artificial intelligence in modern materials science both started. The lecture of the former focused on the nuclear wave function and how we (don’t) deal with it in DFT, but still succeed in optimizing structures. During the lecture on AI we dove into the topics of regularization and learning curves, and extended on different types of ensemble models.

At the end of week 1, this brings me to a total of 12h of lectures. Upwards and onward to week 2.

Permanent link to this article: https://dannyvanpoucke.be/materiomics-chronicles-week-1/

Sep 17 2023

Countdown to Materiomics: Year 2

  • Filed under blog

  • September 17, 2023

Last year, we started a new masters program at Hasselt University called “Materiomics“. It is aimed at bachelor students in chemistry and physics who want to become the materials researchers of the future: interdisciplinary team players with experimental, theoretical, and computational skills ready to build anything made of atoms. There are four specialization tracks developed: Health, Energy, Quantum and Circularity. But passionate students can also develop their own line of study (in consultation with the mentor). The start of this new program was also a new start for myself, as I started as a new tenure track professor materiomics (specialized in computational materials science) assigned to the chemistry department. As a result, I spend most of my time creating new courses for the new first year of the masters program. This year, the second year is launched for the first time, and also here I have a significant contribution. Together with the courses I’m teaching in the bachelor Chemistry program, my first semester will be packed. I’ll be teaching & coordinating 6 courses (25 ECTS), three of them new,  and contributing to others as well:

  1. Introduction to quantum chemistry (2nd Ba. Chemistry)
  2. Quantum and computational chemistry (3rd Ba. Chemistry, new)
  3. Fundamentals of materials modeling (1st Ma. Materiomics)
  4. Properties of functional materials (1st Ma. Materiomics)
  5. Density functional theory: the workhorse of first principles modelling of solids and molecules (2nd Ma. Materiomics, new)
  6. Machine learning and artificial intelligence in modern materials science (2nd Ma. Materiomics, new)

As you can see, the central theme in these courses will be to introduce students into the realm of computational research, often at the quantum mechanical/chemical level.

On top of that, one of the first generation materiomics students will be performing a master thesis in my group, studying the GeV-defect in diamond. Bachelor students in chemistry and physics may join as well later with computational bachelor projects, but that is beyond my personal event horizon of the end of the first semester.

In the following weeks, you will be able to find a weekly review of my endeavors in this regard, providing some insights into what the students in chemistry and the master materiomics (Physics & Chemistry) are learning at Hasselt University.

Permanent link to this article: https://dannyvanpoucke.be/countdown-to-materiomics-year-2/

Jun 08 2023

Hydration sphere structure of architectural molecules: polyethylene glycol and polyoxymethylene oligomers

Authors: Ahmed M. Rozza, Danny E. P. Vanpoucke, Eva-Maria Krammer, Julie Bouckaert, Ralf Blossey, Marc F. Lensink, Mary Jo Ondrechen, Imre Bakó, Julianna Oláh, and Goedele Roos
Journal: Journal of Molecular Liquids 384, 122172 (2023)
doi: 10.1016/j.molliq.2023.122172
IF(2021): 6.633
export: bibtex
pdf: <JMolLiq>

 

Graphical Abstract: PEG or POM, similar in structure though very different in their solvation. Is this due to structure or charge(distribution)?

Abstract

Non-toxic, chemically inert, organic polymers as polyethylene glycol (PEG) and polyoxymethylene (POM) have versatile applications in basic research, industry and pharmacy. In this work, we aim to characterize the hydration structure of PEG and POM oligomers by exploring how the solute disturbs the water structure compared to the bulk solvent and how the solute chain interacts with the solvent. We explore the effect of (i) the C-C-O (PEG) versus CO (POM) constitution of the chain and (ii) chain length. To this end, MD simulations followed by clustering and topological analysis of the hydration network, as well as by quantum
mechanical calculations of atomic charges are used. We show that the hydration varies with chain conformation and length. The degree of folding of the chain impacts its degree of solvation, which is measurable by different parameters as for example the number of water molecules in the first solvation shell and the solvent accessible surface. Atomic charges calculated on the oligomers in gas phase are stable throughout conformation and chain length and seem not to determine solvation. Hydration however induces charge transfer from the solute molecule to the solvent, which depends on the degree of hydration.

 

Permanent link to this article: https://dannyvanpoucke.be/paper-roosg_peg-en/

Jun 02 2023

E-MRS Spring meeting 2023

  • Filed under blog

  • June 2, 2023

In march 2019, Belgium went into COVID-lock down while I attended the yearly diamond conference (SBDD25). Since then, I have been in a bit of a conference lock down myself as well. By visiting the 2023 spring meeting of E-MRS, this lock down has been lifted for international conferences (outside Belgium). Inside Belgium, there was already the DFT-2022 in Brussels, where I was also part of the National Scientific Committee, and of course SBDD26 & SBDD27, which as a diamond researcher you can not miss.

Coming back to Strassbourg for E-MRS brings back some memories, and generated some nice new ones. This year there was a nice Symposium called “Computations for materials – discovery, design and the role of data“[program] which got my full attention. During the first session on AI-accelerated Materials discovery, I had the pleasure to present some of my own work on the Machine Learning of small data sets (cf. papers on the average model, and UV-curable inks). The symposium was nicely coinciding with much of my interest, and showed two (not unexpected, and maybe symposium biased) trends:

  1.  There is an important evolution toward lab-automation and use of robotics (people don’t want to manually build dozens of battery cells or perform hundreds of repetitive synthesis experiments for materials optimization. This shows the future materials scientist, be it a chemist, physicist or engineer will have to become a robotics and/or programming expert as well. This only strengthens me in my vision for our materiomics [NL] students at UHasselt. These skills will be essential for their future scientific career development.
  2. Machine Learning and Artificial Intelligence will play an important role in future materials design. However, we need a better understanding of what we are doing, and not just use any method and accept it as “excellent” because the R² value is high. For now, we can still get away with the latter, but this will not last much longer. It will become more important to have a simple but interpretable model, rather than a complex (over-fitting) Deep Learning Neural Network without understanding of the underlying physics and chemistry. Also here we will have to put in some effort within the materiomics program.

 

So after an interesting International conference, and making some new contacts…it is time to return home, four more courses need to be prepared from scratch for coming academic year.

Permanent link to this article: https://dannyvanpoucke.be/e-mrs-spring-meeting-2023/

Jan 01 2023

Review of 2022

  • Filed under blog

  • January 1, 2023

Happy New Year

2022 has been a year of many firsts. Most importantly, it is the year I started as a tenure track professor (i.e. assistant professor) starting the QuATOMs group at Hasselt University. In addition, this is the first year the new master materiomics program at UHasselt was provided. In this program, I’m responsible for the theoretical and computational components of materials research, and thus teaching several new classes which are unique in the world. Next year, the second master year will start, with more classes to create.

But before we launch into these new and interesting times, lets look back at 2022 one last time, keeping up with  tradition. What have I done during the last year of academic merit.

1. Publications: +4 (and currently a handful in progress)

2. Cover publication: +1

Cover Polymer International: Machine learning on small data sets, application on UV curable inks.

Cover Polymer International: Machine learning on small data sets, application on UV curable inks.

  • Cover Polymer International
    Danny E.P. Vanpoucke, Marie A.F. Delgove, Jules Stouten, Jurrie Noordijk, Nils De Vos, Kamiel Matthysen, Geert G.P. Deroover, Siamak Mehrkanoon, and Katrien V. Bernaerts,
    Polymer International 71(8), i-i (2022),
    doi: 10.1002/pi.6434 {IF(2021)=3.213}

3. Project proposals accepted: +1

  • Digitization of lignin polyurethane development (DigiLignin), in a consortium with Maastricht University and VITO.

4. Completed refereeing tasks: +12

  • Optical Materials
  • Journal of Applied Physics (2x)
  • Frontiers in Physics
  • Journal of Physics: Condensed Matter (2x)
  • Diamond and Related Materials (6x)

5. Conferences & seminars: +3/+1 (Attended & Organised)

With regard to conferences, 2022 was the year everyone wanted to go back to “normalcy”, though COVID is still very much present.

  • SBDD XXVI, Hasselt University, Belgium, March 9th-11th, 2022 [poster presentation, PhD student]
  • BPS-2022, Tabloo Science expo (SCK-CEN), Belgium, May 18th, 2022 [oral presentation]
  • DFT-2022: 19th International Conference on Density Functional Theory and its Applications, Brussels, Belgium, August 28th-September 2nd, 2022. [member of National Organization Committee; poster]
  • VUB-virtual seminar @ALGC group (F. De Proft), Online, November 29th, 2022 [invited seminar presentation]

6. Current size of HIVE:

  • 62K lines of program (code: 69 %)
  • ~100 files
  • 50 (command line) options

7. Hive-STM program:

And now, upward and onward, a new year, a fresh start.

Permanent link to this article: https://dannyvanpoucke.be/review-of-2022/

Dec 01 2022

Elucidating the optimized P2 type Na0.67Mn1−xCuxO2 cathode active material via operando XAS

  • Filed under blog

  • December 1, 2022

Authors: S. Altin, S. Altundag, E. Altin, D. E. P. Vanpoucke, S. Avci, and M. N. Ates
Journal: Journal of Alloys and Compounds 936, 168138 (2023)
doi: 10.1016/j.jallcom.2022.168138
IF(2021): 6.371
export: bibtex
pdf: <J. Alloys Compd.>

Abstract

Here we report on the structural and electrochemical properties of P2-type Na0.67Mn1−xCuxO2 (where x = 0.20–0.50) via various techniques. X-ray diffraction (XRD) reveals a reduction of the unit cell volume upon substitution of Cu elucidated through detailed Rietveld analysis. The cyclic voltammetry (CV) behavior is also affected by the Cu substitution indicating new redox reactions stemming from Cu substitution. Galvanostatic cycling measurements at room temperature show that when x = 0.35 in a P2-type Na0.67Mn1−xCuxO2 cathode active material, the best electrochemical performance is obtained. The Na-ion diffusion rate is found to be strongly dependent upon the environmental temperature. Changes in the
valence state and the local structures of P2-type Na0.67Mn1−xCuxO2 during the charge/discharge are investigated through the operando X-ray absorption spectroscopy (XAS) technique.

 

Permanent link to this article: https://dannyvanpoucke.be/paper-altins_cathode-en/