| Authors: | Danny E. P. Vanpoucke and Sylvia Wenmackers |
| Journal: | Chaos 31, 123131 (2021) |
| doi: | 10.1063/5.0063388 |
| IF(2021): | 3.642 |
| export: | bibtex |
| pdf: | <Chaos> (Open Access) <ArXiv v1> |
| github: | <NortonDomeExplorer> |
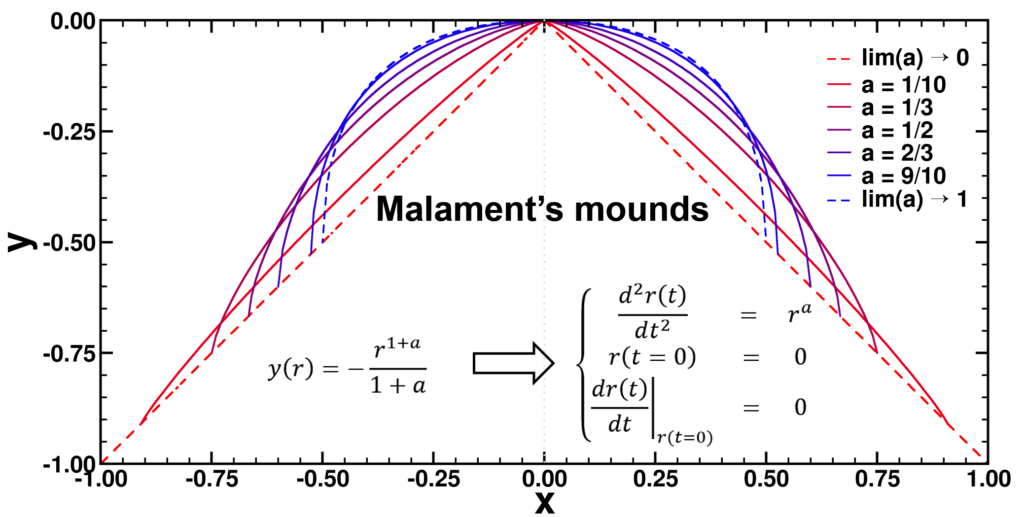 |
| Graphical Abstract: Examples of Malament’s Mounds, of which the Norton Dome is the special case where α=½. |
Abstract
We present a method for assigning probabilities to the solutions of initial value problems that have a Lipschitz singularity. To illustrate the method, we focus on the following toy-example: ,
, and
, with a∈]0; 1[. This example has a physical interpretation as a mass in a uniform gravitational field on a dome of particular shape; the case with a = ½ is known as Norton’s dome. Our approach is based on (1) finite difference equations, which are deterministic; (2) elementary techniques from alpha-theory, a simplified framework for non-standard analysis that allows us to study infinitesimal perturbations; and (3) a uniform prior on the canonical phase space. Our deterministic, hyperfinite grid model allows us to assign probabilities to the solutions of the This allows us to assign probabilities to the solutions of the initial value problem in the original, indeterministic model.
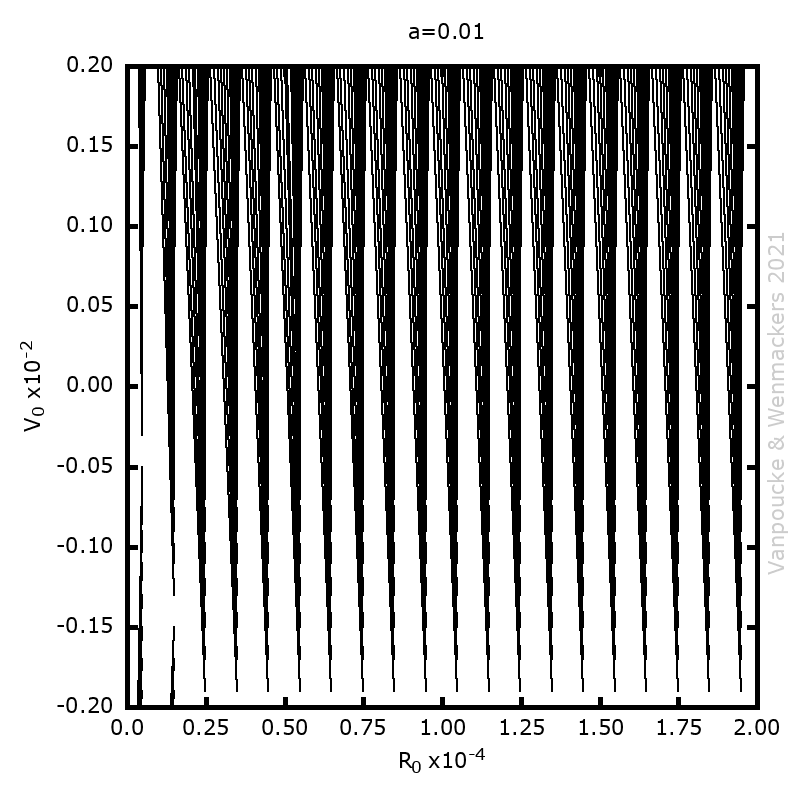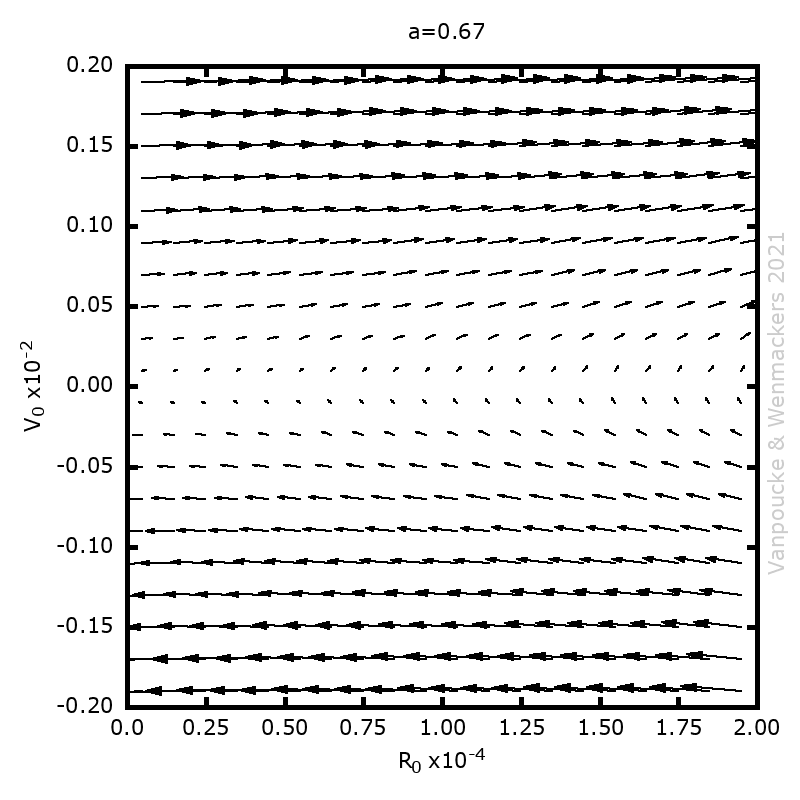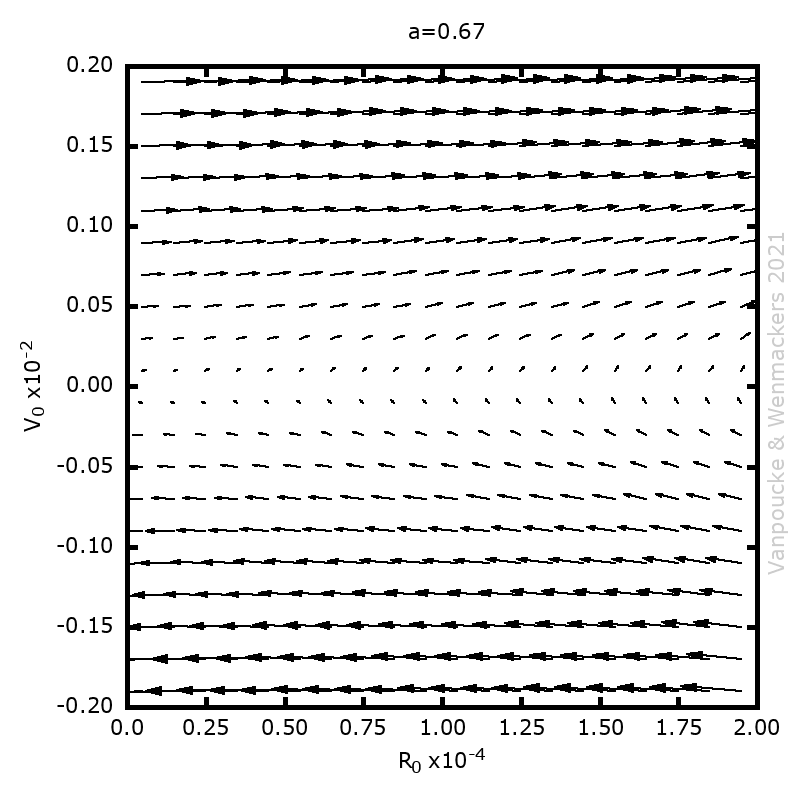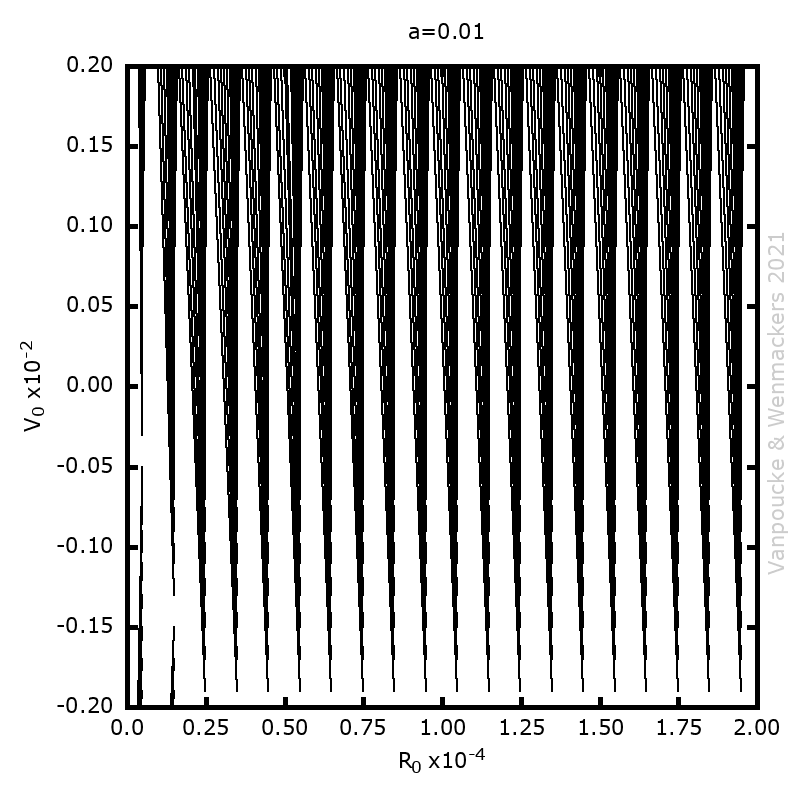
Phase space vector field for all Malament’s mounds