Quantum Holy Grail: The Ground-State
Quantum mechanical calculations provide a powerful tool to investigate the world around us. Unfortunately it is also a computationally very expensive tool to use, which puts a boundary on what is possible in terms of computational materials research. For example, when investigating a solid at the quantum mechanical level, you are limited in the number of atoms that you can consider. Even with a powerful supercomputer at hand, a hundred to a thousand atoms are currently accessible for “routine” investigations. The computational cost also limits the number of configurations/combinations you can calculate.
However, in the end— and often with some blood sweat and tears—these calculations do provide you the ground-state structure and energy of your system. From this point forward you can continue characterizing its properties, life is beautiful and happy times are just beyond the horizon. At this horizon your experimental colleague awaits you. And he/she tells you:
Sorry, I don’t find that structure in my sample.
After recovering from the initial shock, you soon realize that in (materials science) experiments one seldom encounters a sample in “the ground-state”. Experiments are performed at temperatures above 0K and pressures above 0 Pa (even in vacuum :p ). Furthermore, synthesis methods often involve elevated temperatures, increased pressure, mechanical forces, chemical reactions,… which give rise to meta-stable configurations. In such an environment, your nicely deduced ground-state may be an exception to the rule. It is only one point within the phase-space of the possible.
So how can you deal with this? You somehow need to sample the phase-space available to the experiment.
Sampling Phase-Space for Ball-milling synthesis.
For a few years now, I have a very fruitful collaboration with Prof. Rounaghi. His interest goes toward the cheap fabrication of metal-nitrides. Our first collaboration focused on AlN, while later work included Ti, V and Cr-nitrides. Although this initial work had a strong focus on simple corroboration through the energies calculated at the quantum mechanical level, the collaboration also allowed me to look at my data in a different way. I wanted to “simulate” the reactions of ball-milling experiments more closely.
Due to the size-limitations of quantum mechanical calculations I played with the following idea:
- Assume there exists a general master reaction which describes what happens during ball-milling.
X Al + Y Melamine → x1 Al + x2 Melamine + x3 AlN + …
where all the xi represent the fractions of the reaction products present.
- With the boundary condition that the number of particles needs to be conserved, you end up with a large set of (x1,x2,x3,…) configurations which each have a certain energy. This energy is calculated using the quantum mechanical energies of each product. The configuration with the lowest energy is the ground state configuration. However, investigating the entire accessible phase-space showed that the energies of the other possible configurations are generally not that much higher.
- What if we used the energy available due to ball-milling in the same fashion as we use kBT? And sample the phase-space using Boltzmann statistics.
- The resulting Boltzmann distribution of the configurations available in the phase-space can then be used to calculate the mass/atomic fraction of each of the products and allow us to represent an experimental sample as a collection of small units with slightly different configurations, weighted according to their Boltzmann distribution.
This setup allowed me to see the evolution in end-products as function of the initial ratio in case of AlN, and in our current project to indicate the preferred Iron-nitride present.
Grid-sampling vs Monte-Carlo-sampling
Whereas the AlN system was relatively easy to investigate—the phase space was only 3 dimensional— the recent iron based system ended up being 4 dimensional when considering only host materials, and 10 dimensional when including defects. For a small 3-4D phase-space, it is possible to create an equally spaced grid and get converged results using a few million to a billion grid-points. For a 10D phase-space this is no longer possible. As you can no longer keep all data-points (easily) in storage during your calculation (imagine 1 Billion points, requiring you to store 11 double precision floats or about 82Gb) you need a method that does not rely on large arrays of data. For our Boltzmann statistics this gives us a bit of a pickle, as we need to have the global minimum of our phase space. A grid is too course to find it, while a simple Monte-Carlo just keeps hopping around.
Using Metropolis’s improvement of the Monte-Carlo approach was an interesting exercise, as it clearly shows the beauty and simplicity of the approach. This becomes even more awesome the moment you imagine the resources available in those days. I noted 82Gb being a lot, but I do have access to machines with those resources; its just not available on my laptop. In those days MANIAC supercomputers had less than 100 kilobyte of memory.
Although I theoretically no longer need the minimum energy configuration, having access to that information is rather useful. Therefore, I first search the phase-space for this minimum. This is rather tricky using Metropolis Monte Carlo (of course better techniques exist, but I wanted to be a bit lazy), and I found that in the limit of T→0 the algorithm will move toward the minimum. This, however, may require nearly 100 million steps of which >99.9% are rejected. As it only takes about 20 second on a modern laptop…this isn’t a big issue.
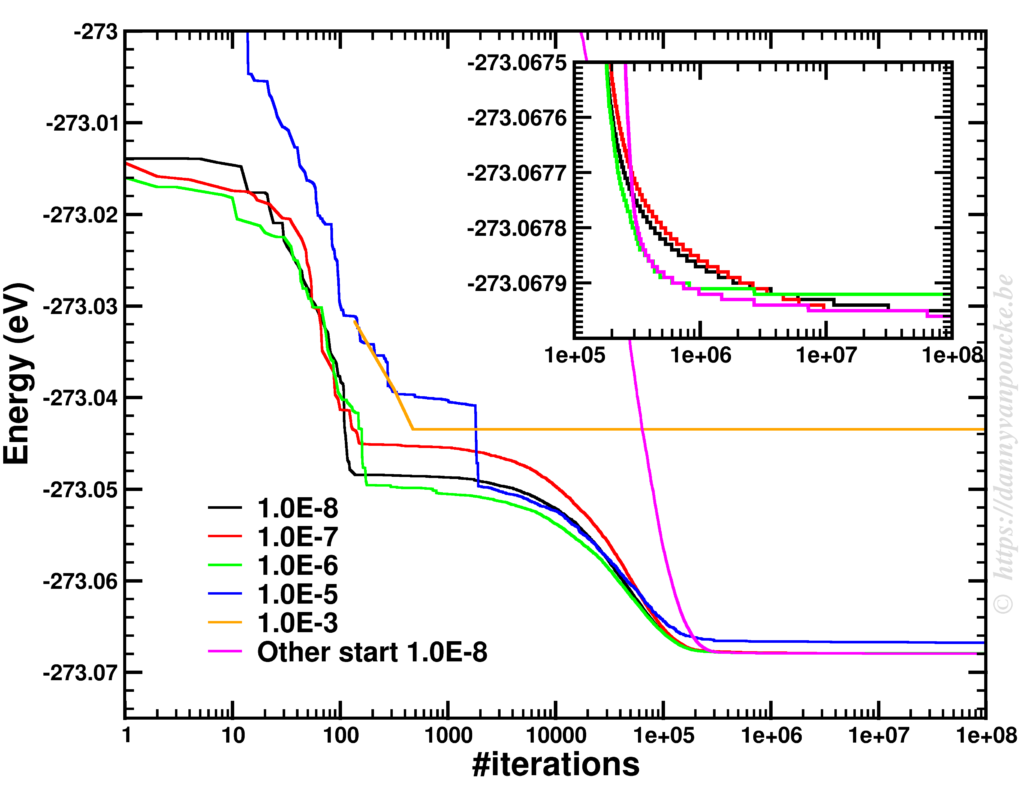
Finding a minimum using Metropolis Monte Carlo.
Next, a similar Metropolis Monte Carlo algorithm can be used to sample the entire phase space. Using 109 sample points was already sufficient to have a nicely converged sampling of the phase space for the problem at hand. Running the calculation for 20 different “ball-milling” energies took less than 2 hours, which is insignificant, when compared to the resources required to calculate the quantum mechanical ground state energies (several years). The figure below shows the distribution of the mass fraction of one of the reaction products as well as the distribution of the energies of the sampled configurations.
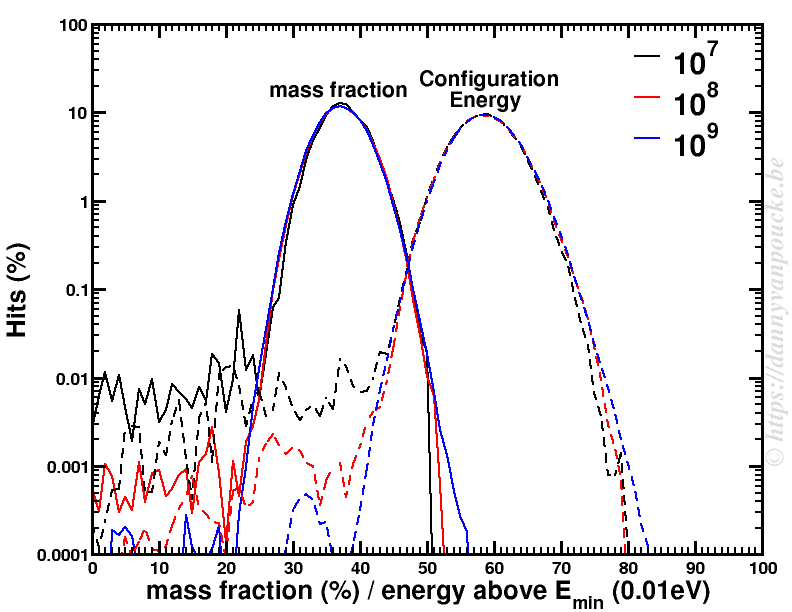
Metropolis Monte Carlo distribution of mass fraction and configuration energies for 3 sets of sample points.
This clearly shows us how unique and small the quantum mechanical ground state configuration and its contribution is compared to the remainder of the phase space. So of course the ground state is not found in the experimental sample but that doesn’t mean the calculations are wrong either. Both are right, they just look at reality from a different perspective. The gap between the two can luckily be bridged, if one looks at both sides of the story.