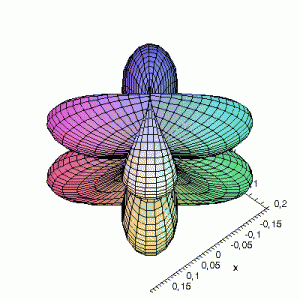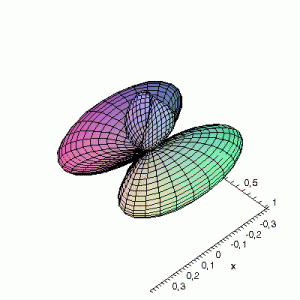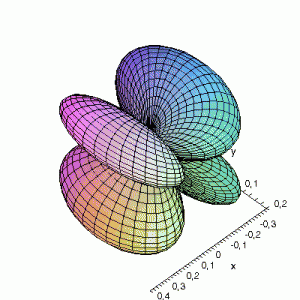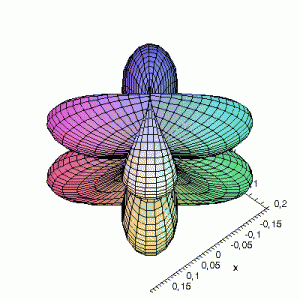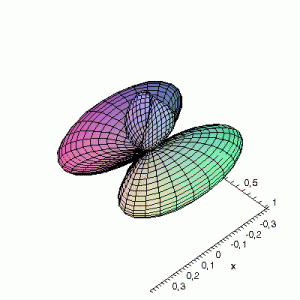Tag: orbitals

Jan 01 2010

f-orbitals

3D f-Orbitals

3D gnuplot-gif-animations of the f-orbitals S03(θ,φ), S23(θ,φ) and
S33(θ,φ). In the images presented, the blue part represents the positive phase, and the red part the negative phase. Note that in gnuplot, the spherical coordinate θ is defined as π/2 – θ. Other than that the definitions of φ and θ coincide with those used in Griffiths’ Introduction to Quantum Mechanics.

For those interested: animations in gnuplot are only available for gnuplot versions > 4.0 (which at the moment of making these animations, was still in beta version).

S03(θ,φ)


Animated f-orbitals (gnuplot) of the S03 function. Different phases indicated in red and blue.

S23(θ,φ)


Animated f-orbitals (gnuplot) of the S23 function. Different phases indicated in red and blue.

S33(θ,φ)


Animated f-orbitals (gnuplot) of the S33 function. Different phases indicated in red and blue.

Permanent link to this article: https://dannyvanpoucke.be/f-orbitals-en/

Jan 01 2000

d-orbitals

3D d-Orbitals

3D Maple-images of the d-orbitals S02(θ,φ), S12(θ,φ) en S22(θ,φ). Note that the spherical coordinates (θ and φ) used by Maple are reversed compared to the definitions used in Griffiths’ Introduction to Quantum Mechanics (the latter being the more standard definition in physics and mathematics courses).

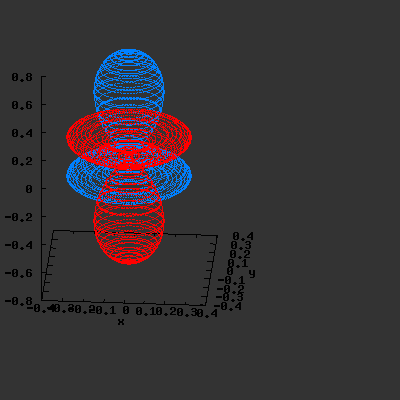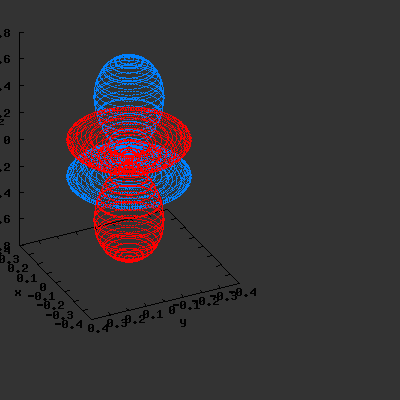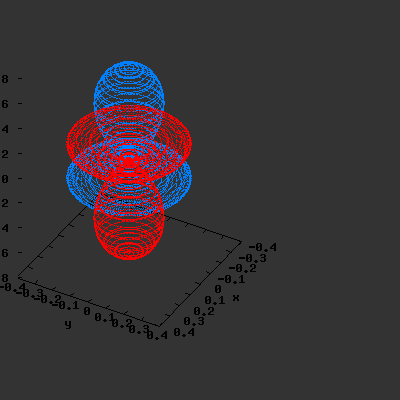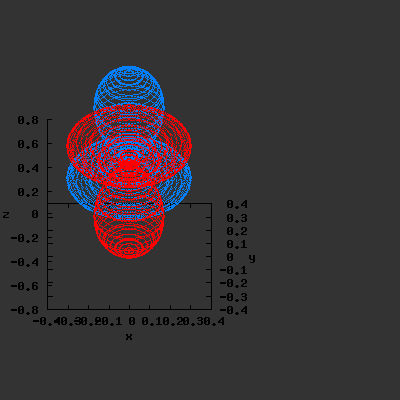
S02(θ,φ)

>  plot3d(abs(3*cos(phi)*cos(phi)-1),theta=0..Pi,phi=0..2*Pi,
grid=[60,60],coords=spherical,axes=frame,labels=[x,y,z]);

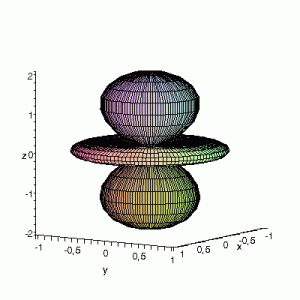
Maple 3D representation of atomic d-orbitals defined by the S02 function.

S12(θ,φ)

>  plot3d(abs(sin(phi)*cos(phi)*cos(theta)),theta=0..2*Pi,phi=0..Pi,
grid=[60,60],coords=spherical,axes=frame,labels=[x,y,z]);

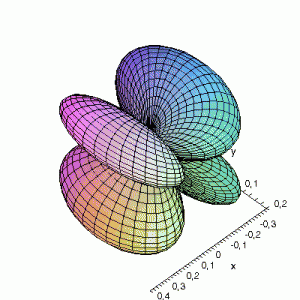
Maple 3D representation of atomic d-orbitals defined by the S12 function.

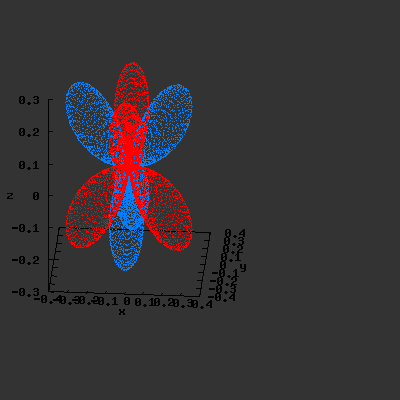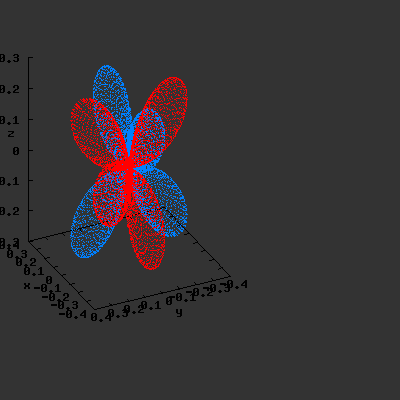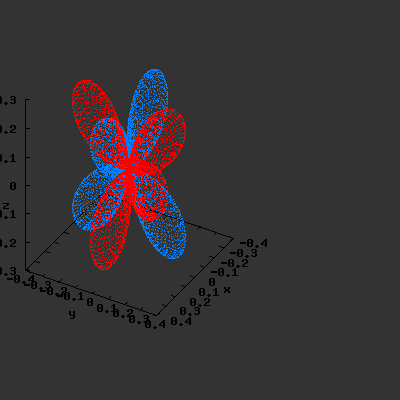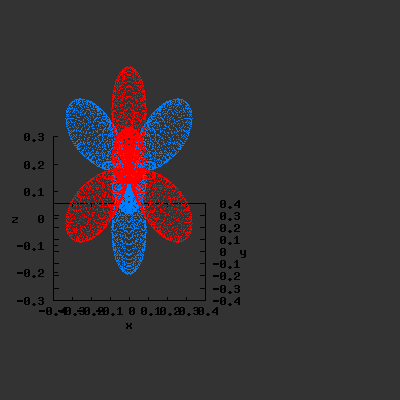
S22(θ,φ)

>  plot3d(abs(sin(phi)*sin(phi)*cos(2*theta)),theta=0..2*Pi,phi=0..Pi,
grid=[60,60],coords=spherical,axes=frame,labels=[x,y,z]);

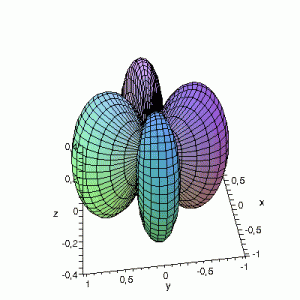
Maple 3D representation of atomic d-orbitals defined by the S22 function.

Effect of exchanging θ and φ

Maple assumes the first angle given is the angle in the xy-plane; the second angle is with regard to the z-axis. This makes that you have to be very careful when giving Maple the θ and φ angles, and make sure that their definitions are the same. If the definitions
are reversed: I.e. if we use the variable θ as the variable φ and vice versa, the resulting plots become something quite different. This goes for all available plotting programs (Maple, gnuplot…); make sure you certain that what you think you enter is also what the program thinks you have entered. If not you could end up with surprising results. The same images as above, but now with θ and φ exchanged:


Wrong Maple 3D representation of atomic d-orbitals defined by the S02 function. The theta and phi angles are exchanged.
Wrong Maple 3D representation of atomic d-orbitals defined by the S12 function. The theta and phi angles are exchanged.

Wrong Maple 3D representation of atomic d-orbitals defined by the S22 function. The theta and phi angles are exchanged.

Permanent link to this article: https://dannyvanpoucke.be/d-orbitals-en/