Phonons: shake those atoms

In physics, a phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, like solids and some liquids. Often designated a quasi-particle, it represents an excited state in the quantum mechanical quantization of the modes of vibrations of elastic structures of interacting particles.

— source: wikipedia

Or for simplicity: sound waves; the ordered shaking of atoms or molecules. When you hit a metal bell with a (small) hammer, or make a wineglass sing by rubbing the edges, you experience the vibrations of the object as sound. All objects in nature (going from atoms to stars) can be made to vibrate, and they do this at one or more specific frequencies : their eigenfrequencies or normal frequencies.

Also single molecules, if they are hit (for example by another molecule bumping into them) or receive extra energy in another way, start to vibrate. These vibrations can take many forms (elongating and shortening of bonds, rotating of parts of the molecule with respect to other parts, flip-flopping of loose ends, and so forth) and give a unique signature to the molecule since each of these vibrations (so-called eigen-modes) corresponds with a certain energy given to the molecule. As a result, if you know all the eigen-modes of a molecule, you also know which frequencies of infrared light they should absorb, which is very useful, since in experiment we do not “see” molecules (if we see them at all) as nice ball-and-stick objects.

From the computational point of view, this is not the only reason why in molecular modeling the vibrational frequencies of a system (i.e. the above eigen-modes) are calculated. In addition, they also tell if a system is in its ground state (which is what one is looking for most of the time) or not. Although this tool has wide-spread usage in molecular modeling, it is seldom used in ab initio solid state physics because of the associated computational cost. In addition, because of the finite size of the unit cell, the reciprocal space in which phonons live also has a finite size, in contrast to the single point for a molecule…making life complex. 😎

Phonons at the 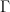-point.

In my work on Metal Organic Frameworks, I came to two unhappy conclusions: (1) the relative cost of such a phonon calculation is reasonable (only because a good structure optimization already takes a few thousand ionic steps) and (2) such calculations are required if you really want to be sure you end up in the ground state (there are too many micro-variations of the structure which are nearly undetectable in experiment and invisible to our structure optimizers, but modify the stability of the system a lot.)

Most high level ab initio solid state programs allow one to calculate the energy levels of the vibrations at the center of the reciprocal space (i.e. the only remaining point of the reciprocal space when looking at molecules). However, if you want to obtain a full phonon spectrum of a solid, you also need to know the energy of the vibration modes in all other points of the reciprocal space (actually, the first Brillouin zone suffices), we will call them q-points. Fortunately, both can be obtained from the dynamical matrix D(q), an extension of the Hessian matrix of the energy :

for wave-vector q (yes, it is the same as the q-point above), with i,j properties of the and  atom of the system. Only for the center of the reciprocal space (-point: q=(0,0,0)) the matrix D is real, for all other points, D is a complex matrix. The eigenvalues of this matrix are the square of the vibrational frequencies we are interested in. Negative eigenvalues (i.e. imaginary frequencies) are often an indication of the non-convergence or instability in the structure. In other cases they are just an indication of numerical artifacts due to too low accuracy in the calculation.

There are many different methods for diagonalizing matrices; quite often specialized for specific types of matrices (symmetric, band-diagonal, etc). However, since I did not want to worry about this, and because the dynamical matrices I am interested in are relatively small, I opted to use an Singular Value Decomposition (SVD). This method is very robust, but unfortunately it does not contain a sign for the eigenvalues, since the singular values you get are actually the square roots of the eigenvalues of . Luckily, the sign-problem can be resolved by solving the matrix equation

and checking which sign for the eigenvalue gives a result closest to the zero-vector, for the eigenvector . For the -point phonon frequencies, the SVD-implementation found in numerical recipes is sufficient, and after implementing the small hack to recover the sign, I was able to get the exact same frequencies as those directly available in the ab initio code (VASP) …phew.

Phonons in the remainder of the Brillouin-zone

Ball-and-stick representation of diamond in two different unit cells. Left: primitive unit cell containing two atoms. All atoms at the vertices are periodic copies of the same one. Right: Conventional cubic unit cell containing eight atoms. Atoms at opposing faces are periodic copies, while all atoms at the vertices are periodic copies of the same atom.

In this second step, the exponential part (which is now no longer trivially equal to 1) of the dynamical matrix needs to be explicitly included.
Because the dynamical matrix is a complex matrix, the numerical recipes version of SVD is no longer sufficient. Luckily, the LAPACK library contains a complex SVD. A good tutorial on how to install LAPACK using a native windowsYes, Windows, even though I am a computational physicist. I can get a BOD on both types of OS, so I prefer the one that at least gives error-messages ;). gfortran compiler was a life-saver. After having LAPACK compiled, you just need to link the libraries. If you use code::blocks just go to

settings > Compiler > Linker Settings

and add liblapack.a and librefblas.a .

To test everything, I used a very simple system: Bulk diamond, with only two atoms in the primitive unit cell, the dynamical matrix is only , allowing one to check the numbers during debugging. As said, the phonons at the -point were correct, however, upon turning my attention to high symmetry lines in the first Brillouin zone I got the left picture below, woeps.

Using a primitive diamond unit cell with only two atoms, simple extension of the dynamical matrix leads to flat bands (a). Taking into account that the off-diagonal terms refer to the interaction between the two C atoms, and that each C atom experiences 4 such interactions, the dispersion of the bands becomes non-zero (b). Using a larger unit cell such as the conventional 8 atom cell, much of those interactions get explicitly introduced in the dynamical matrix (dotted lines in (c) ), while some are still missing for the atoms at the edge of the cell. The effect of their inclusion is shown by the red solid lines.(c) The blue solid lines show the bands of the primitive two atom cell (also shown in (b)) for comparison.

There is no dispersion whatsoever. On the other hand, if we use the conventional cubic unit cell with 8 atoms, there clearly is dispersion of the bands (cf. figure (c) the dotted lines). Looking back at the very simple dynamical matrix for our 2-atom system, we note that the diagonal blocks describe what in other fields may be called self-interactions, and the off-diagonal blocks describe the interaction between the two atoms. In the case of the diamond example, we should note that each carbon has 4 nearest neighbors instead of only 1; the 4 bonds are shown in the primitive cell for the second atom. As such, the term should be a sum of 4 of these terms with the term running over the 4 nearest neighbors. The result is shown in the picture above in the middle panel: no more flat bands. 🙂

But what happens with the conventional cell? Because most atoms already have all their nearest neighbors included the effect is much less pronounced, but still clearly present (the dotted lines and the red solid lines in the right panel above). Comparison to the band structure of the primitive cell shows this one to be already quite decent, despite its limitations.

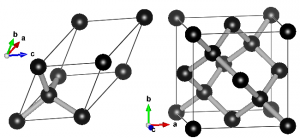
The phonon density of states for diamond, calculated using a dynamical matrix based on a primitive 2-atom cell, and a conventional cubic 8-atom cell. A Gaussian smearing of 0.3 THz is used to smooth the curves.

Extending the computational cost further, we can also sample the entire first Brillouin zone (instead of only points along the high symmetry lines) and create a phonon density of states. The main hurdle in its implementation, is finding an algorithm for generating a set of q-points which only sample the first Brillouin zone.

A brute-force approach creating a homogeneous distribution of q-points over a region larger than the first Brillouin zone, and then only selecting those q-points which are inside the first Brillouin zone is relatively easy to implement, although efficiency becomes an issue when you try to run through one million q-points on a 7-year old netbook.

However, for now it suffices, and will allow me to generate phonon band structures and densities of state for my MOFs, and calculate thermal contributions due to these phonons…to be continued.