One of the main differences between theory and computational research is the fact that the latter has to deal with finite resources; mainly time and storage. Where theoretical calculations involve integrations over continuous spaces, infinite sums and basis sets, computational work performs numerical integrations as weighted sums over finite grids and cuts of infinite series. As an infinite number of operations would take an infinite amount of time, it is clear why numerical evaluations are truncated. If the contributions of an infinite series become smaller and smaller, it is also clear that at some point the contributions will become smaller than the numerical accuracy, so continuation beyond that point is …pointless.
In case of ab initio quantum mechanical calculations, we aim to get as accurate results at an as low computational cost as possible. Even with the current availability of computational resources, an infinite sum would still take an infinite amount of time. In addition, although parallelization can help out a lot in getting access to additional computational resources during the same amount of real time, codes are not infinitely parallel, so at some point adding more CPU’s will no longer speed up the calculations. Two important parameters in quantum mechanical calculations to play with are the basis set size (Or kinetic energy cut off, in case of plane wave basis sets. In which case this can also be related to the real space integration grid) and the integration grid for the reciprocal space (the k-point grid).
These two parameters are not unique to VASP, they are present in all quantum mechanical codes, but we will use VASP as an example here. The example system we will use is the α-phase of Cerium, using the PBE functional. The default cut-off energy used by VASP is 299 eV.
1. Basis set size/Kinetic energy cut-off
What a basis set is and how it is defined depends strongly on the code. As such you are referred to the manual/tutorials of your code of interest.(VASP workshop) One important thing to remember, however, is the fact that although a plane wave basis set is “nicely behaved” (bigger basis = more accurate result) this is not true for all types of basis sets (Gaussian basis sets are an important example here).
How do you perform a convergence test?
-
Get a geometry of your system of interest.
This does not need to be a fully optimized geometry, an experimental geometry or a reasonable manually constructed geometry will do fine, as long as it gives you a converged result at the end of your static calculation. A convergence test should not depend on the exact geometry of your system. Rather it should tell you how well your setting converges your result with regard to the energy found on the potential energy surface.
-
Fix all other settings
(to reasonable values, although the settings should—to make your life somewhat sane—be independent with regard to convergence testing).
VASP specific parameters of importance:- PREC : should be at least normal, but high or accurate are also possible
- EDIFF : a value of 1.0E-6 to 1.0E-8 are reasonable for small systems. Note that this value should be much smaller than the accuracy you wish to obtain.
- NSW = 0; IBRION = -1 : It should be static calculations.
- ISPIN : If you intend to perform spin polarized calculations, you should also include this in your convergence tests. Yes it increases the computational cost, but remember that convergence tests will only take a fraction of the computational costs of your project, and can save you a lot of work and resources later on.
- NBANDS : You may want to manually fix the number of electronic bands, which will allow for comparison of timing results.
- LCHARG = .TRUE. ; ICHARG = 1: If you are not that interested in timing (or use average time of electronic loops instead of total CPU time), and want to speed things up a bit, you can use the electron density from a cheaper calculation as a starting point.
- KPOINTS-file: use a non-trivial k-point set. e. unless you are looking at a molecule or very large system do not use the Gamma-point only.
-
Loop over a set of kinetic energy cut-off values.
These should be a simple static calculation. Make sure that each of the calculations finishes successfully, otherwise you will not be able to compare results and check convergence.
-
Collect relevant data and check the convergence behavior.
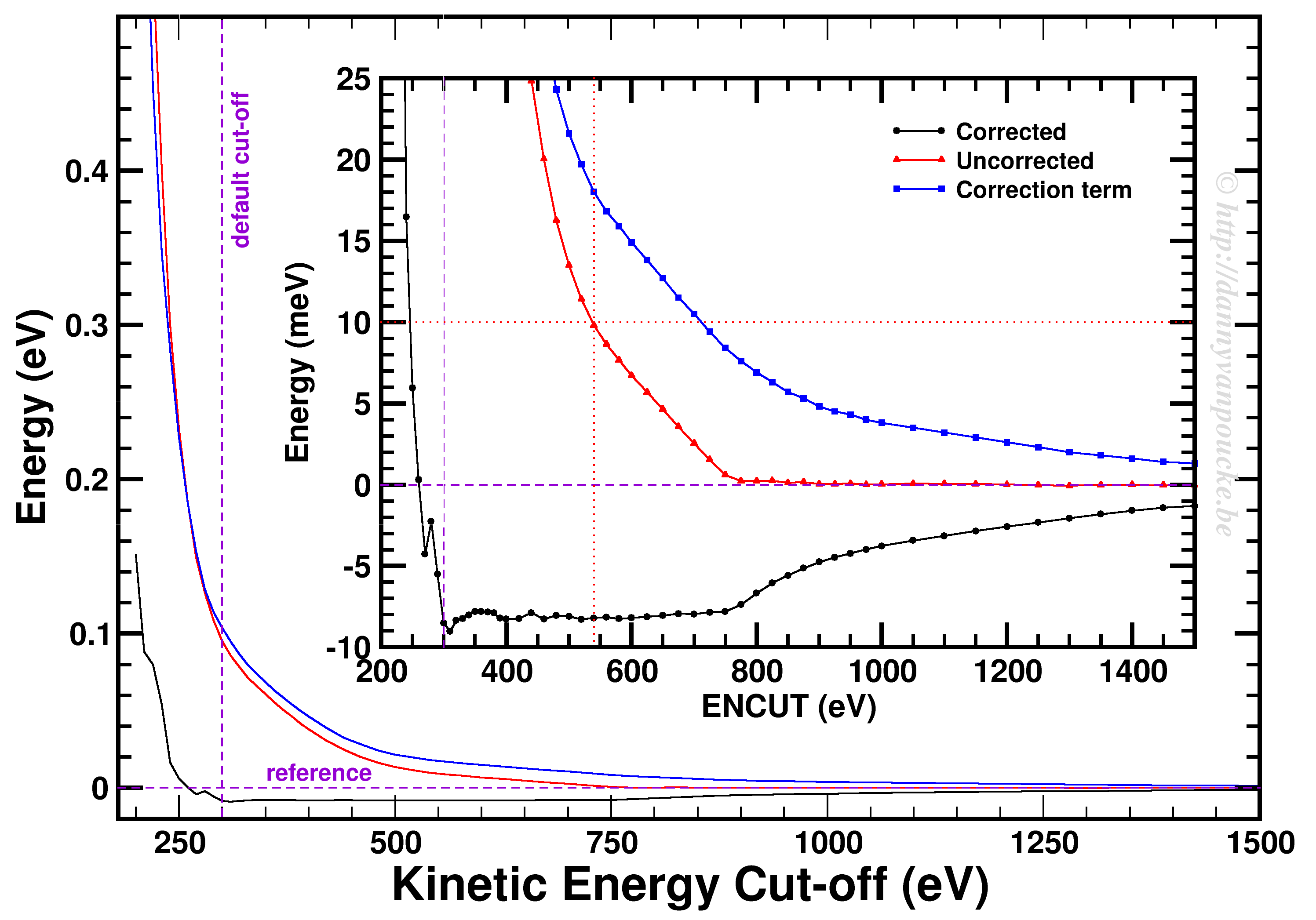
Convergence of the kinetic energy cut-off for alpha Ce using the PBE functional and a 9x9x9 k-point grid.
In our example, we used a 9x9x9 k-point set. Looking at the example, we first of all see how smoothly the total energy varies with regard to the ENCUT parameter. In addition, it is important to note that VASP has a correction term (search for EATOM in the OUTCAR file) implemented which greatly improves the energy convergence (compare the black and red curves). Unfortunately, it also leads to non-variational convergence (i.e. the energy does not become strictly smaller with increasing cut-off) which may lead to some confusion. However, the correction term performs really well, and allows you to use a kinetic energy cut-off which is much lower than what you would need to use without. In this case, the default cut-off misses the reference energy by about 10 meV. Without the correction, a cut-off of about 540 eV (almost double) is needed. From ENCUT=300 to 800 eV, you observe a plateau, so using a higher cut-off will not improve the energy much. However, other properties, such as the calculated forces or the hessian may improve in this region. For these parameters a higher cut-off may be beneficial, and their convergence as function of ENCUT should be checked if important for your work.
2. K-point set
Similar as for the kinetic energy cut-off, if you are working with a periodic system you should check the convergence of your k-point set. However, if you are working with molecules/clusters your Brillouin zone reduces to a single point, so your k-point set should only consist of the Gamma point and no convergence testing is needed. More importantly, if you use a larger k-point set for such systems (molecules/clusters) you introduce artificial interaction between the periodic copies which should be avoided at all cost.
For bulk materials a k-point convergence check has a similar setup as the basis set convergence check. The main difference being the fact that for these calculation the basis set is kept constant (VASP: ENCUT = default cut-off, manually set) and the k-point set is varied. As such, if you are new to quantum mechanical calculations, or start using a new code, you can combine the two convergence checks and study the convergence behavior on a 2D surface.
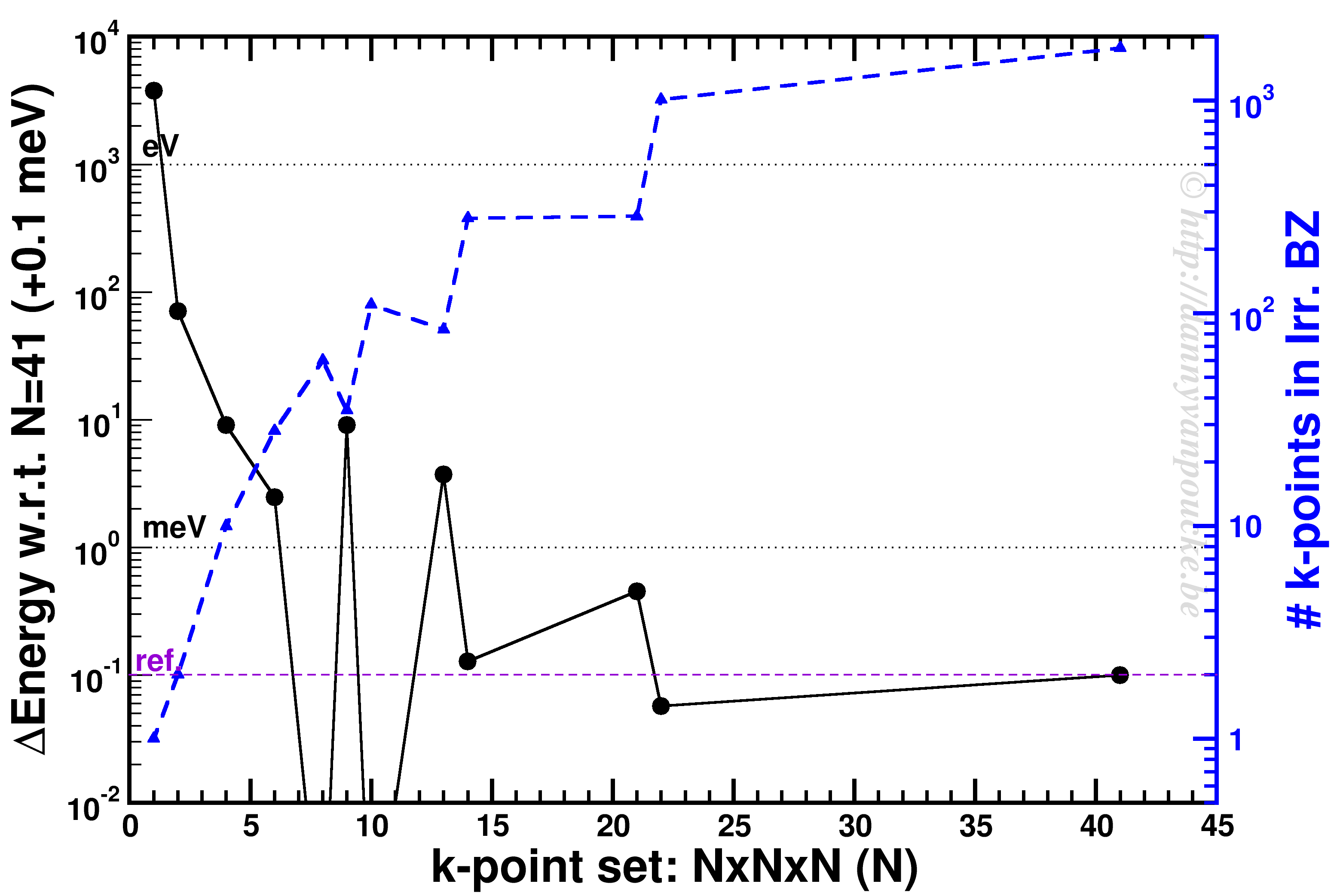
K-point convergence of alpha-Cerium using the PBE functional and ENCUT=500 eV.
In our example, ENCUT was set to 500 eV. It is clear that an extended k-point set is important for small systems, as the Gamma-point only energy can be off by several eV. This is even the case for some large systems like MOFs. An important thing to remember with regard to k-point convergence, is the fact that this convergence is not strictly declining, it may show significant oscillations overshooting and undershooting the converged value. A convergence of 1 meV or less for the entire system is a goal to aim for. An exception may be the most large systems, but even then one should keep in mind the size of the energy barriers in that system. Using flexible MOFs as an example which show a large-pore to narrow-pore transition barrier of 10-20 meV per formula unit, k-point convergence should be much below this. Otherwise your system may accidentally cross this barrier during relaxation.
The blue curve shows the number of k-points in the irreducible Brillouin zone. For standard density functional theory calculations (LDA and GGA, not hybrid functionals) this is a measure of the computational cost, as the k-points can be calculated fully independently in parallel (and yes the blue scale is a log-scale as well). Because the first orders of magnitude in accuracy are quickly crossed ( from Gamma to 6x6x6 the energy error goes from the order of eV to meV) while the number of k-points doesn’t grow that quickly (from 1 to 28). As a result, one often performs structure optimizations in a stepped fashion, starting with a coarse grid steadily increasing the grid (unless pathological behavior is expected… MOFs again…yes, they do leave you with nightmares in this regard).
3. Conclusions
Convergence testing is necessary, in theory, for each and every new system you look into. Luckily, VASP behaves rather nicely, such that over time you will know what to expect and your convergence tests will reduce in size significantly and become more focused. In the examples above we used the total energy as a reference, but this is not always the most important aspect to consider. In some cases you should check the convergence as function of the accuracy of the forces. In that case you generally will end up with more stringent criteria as energy converges rather nicely and quickly.
May your convergence curves be smooth and quick.


3 comments
Hi
I am Archana Sharma, Ph. D. student at Jamia Millia Islamia, New Delhi, India. I can find your post to be very informative. However, I could not understand few things in the section ENCUT optimization. Which values of energy are plotted on the Y-axis against different cutoffs such that zero is taken as the reference ? And how come 540 eV is the optimized ENCUT value without correction?
Hope to get enlightened on my doubts.
Thanks in advance !
Author
Hello Archana,
The Y-axis presents the total energy of a unit cell of alpha-Ce. The curves present the total energy as calculated by VASP (black), the correction term used by VASP (blue) and the uncorrected variational energy as would be obtained without the correction term (red). The zero reference is set to the energy of the variational (uncorrected) energy using an ENCUT of 1500 eV (No way you will use such a high cut off for production calculations, as your computational cost will be huge.).
What I show in the plot is the following. Assume you want to have an energy within 10meV of the converged value (i.e. our 1500 eV reference). Then without the correction VASP is using, you would need to set ENCUT to at least 540 eV. However, due to the correction implemented in VASP you can use an ENCUT as low as 300 eV. This give you a significant reduction in the computational cost: it goes from 34 second (550eV) down to 22.5 seconds (300eV) a 30% reduction in cost, but same quality energies. In this specific case the impact seems small, but is will count for serious projects. A healthy computational project easily take a few years to a few decades of calculation time. Imagine it taking 50% longer, of having to apply/pay for 50% more calculation time.
Kind regards,
Danny
Dear Danny
Thanks for the informative and useful tutorial on VASP. Is it possible to provide a tutorial on optimization without EOS fitting ?