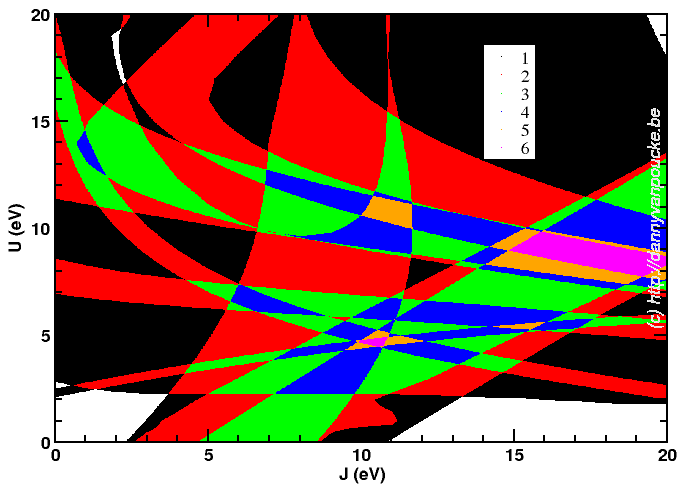
Although it looks a bit like a modern piece of art, it is one more attempt at trying to find an optimum combination of parameters.
I’m currently trying to find “the best choice” for U and J for a DFT+U based project… DFT??? Density Functional Theory. This is an approximate method which is used in computational materials science to calculate the quantum mechanical behavior of electrons in matter. Instead of solving the Schrödinger equation, known from any quantum mechanic course, one solves the Hohenberg-Kohn-Sham equations. In these equations it are not the electrons which play a central role (which they do in the Schrödinger equations) but the electron density. Hohenberg, Kohn and Sham were able to show that their equations give the exact same results as the Schrödinger equations. There is, however, one small caveat: you need to have an “exact” exchange-correlation functional (a functional is just a function of a function). Unfortunately there is no known analytic form for this functional, so one needs to use approximated functionals. As you probably guessed, with these approximate functionals the solution of the Hohenberg-Kohn-Sham equations is no longer an exact solution.
For some molecules or solids the error is much larger than average due to the error in the exchange-correlation functional. These systems are therefore called “strongly-correlated” systems. Over the years, several ways have been devised to solve this problem in DFT. One of them is called DFT+U. It entails adding additional coulomb interactions (Hubbard-U-potential) between the “strongly interacting electrons”. However this additional interaction depends on the system at hand, so one always needs to fit this parameter against one of more properties one is interested in. The law of conservation of misery, however, makes sure that improving one property goes hand in hand with a deterioration of another property.
Since actual DFT+U has two independent parameters (U and J, though for many systems they can be dependent reducing to a single parameter) I had quite some fun running calculations for a 21×21 grid of possible pairs. Afterward, collecting the data I wanted to use for fitting purposes took my script about 2h! 😯 Unfortunately the 10 properties of interest I wanted to fit give optimum (U,J)-pair all over the grid. In the picture above, you see my most recent attempt at trying to deal with them. It shows for the entire grid how many of the 10 properties are reasonably well fit.There are two regions which fit 6 properties; One around (U,J)=(5,10) and another around (U,J)=(8.5,17.5). There will be more work before this gives a satisfactory result, the show will go on.

