After having set up our new project in the first session of this tutorial, we now come to an important second step: choosing and creating our Objects. In OOP, the central focus is not a (primitive) variable or a function, but “an object”. In Object Oriented Programming (OOP) most if not all variables and functions are incorporated in one or more (types of) objects. An object, is just like a real-life object; It has properties and can do things. For example: a car. It has properties (color, automatic or stick, weight, number of seats,…) and can do things (drive, break down, accelerate,…). In OOP, the variables containing the values that give the color, weight, stick or not,… of the car are called the properties of the car-object. The functions that perform the necessary calculations/modifications of the variables to perform the actions of driving, breaking down,… are called the methods.
Since we are still focusing on the opinion dynamics paper of Sobkowicz, let us use the objects of that paper to continue our tutorial. A simplified version of the research question in the paper could be as follows:
How does the (average) opinion of a population of agents evolve over time?
For our object-based approach, this already contains much of the information we need. It tells us what our “objects” could be: agents. It gives us properties for these objects: opinion. And it also tells us something of the methods that will be involved: opinion…evolve over time.
Let us now put this into Fortran code. A class definition in Fortran uses the TYPE keyword, just like complex data types.
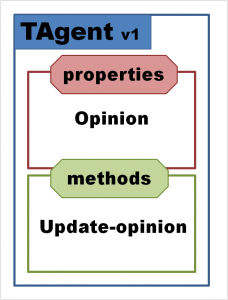
- Type, public :: TAgentClass
- private
- real :: oi !< opinion
- contains
- private
- procedure, pass(this), public :: getOpinion
- procedure, pass(this), public :: setOpinion
- procedure, pass(this), public :: updateOpinion
- end type TAgentClass
A Fortran class consist out of two parts: the first part lists all the properties, while the second (optional) part, following the contains keyword, lists the methods of the object. Note that I start each part with the private keyword, to indicate that by default everything should be hidden for the outside world. This is part of the OOP concept of encapsulation and data hiding. In data hiding one allows the outside world access to a property of an object through accessor and mutator methods (set and get). This way the programmer can make sure modification of a given property is always performed in the intended fashion. Furthermore, the use of accessors allows for properties to be internally stored in a different fashion, or not at all, and calculated on the fly when requested. As such, the opinion variable oi is outside the agent-object only accessable through the method getOpinion, and can only be modified through the method setOpinion. The method updateOpinion will perform the opinion update. Each of these methods has the public keyword, which means that they are accessible from outside the TAgentClass-object.
There are two more important keywords at play in the above example: procedure and pass. As you may have noted, our description of the methods does not contain any information on which parameters they take, if they are functions or subroutines. The only information given is their name, and that they are procedures, which just means that it are either functions or subroutines. The advantage of this approach is that you can easily change your function/subroutine calling sequence without the need for updating your class definition. The pass(this) keyword is a way of telling Fortran that this procedure will take at least one variable (which doesn’t need to be provided during the procedure call) called ‘this’(you may name it whatever you want) which is your actual TAgentClass-object. This is a major difference with languages like C++, where the this-pointer (or self in case of pascal) is implicitly present.
The setup of our module containing this class will then look like this:
As is clear in the code above, the “procedures” are just functions and subroutines known from standard Fortran 90/95, only the use of the class keyword is new. The class indication is similar to the type indication, but extends on it. The concept of inheritance allows one to derive one class from another. For example the classes TCar and TPlane could both be child classes of the class TVehicle, they contain all methods and properties of the TVehicle class plus some specific to the TCar or TPlane class. If a function now has a parameter of the TVehicle class, then it means that also objects of the types TCar and TPlane are acceptable input. We will come back to this in a future tutorial when we discuss inheritance.
Returning to the paper of Sobkowicz,we find that there are other variables involved in the simulation:
- Tolerance threshold d: This parameter defines if opinions update to a new value or remain the same. In this paper, this parameter is specific for each agent, and a function of it’s opinion:
d = dmax – |opinion|L(dmax-dmin)
- Threshold range dmin, dmax: Two global variable which define in what range the d may have a value
- Exponent L : Another global variable which defines how d varies through the range.
- Constant parameter µ : which controls the speed of convergence during the opinion updates, and is a real value between 0 and 0.5
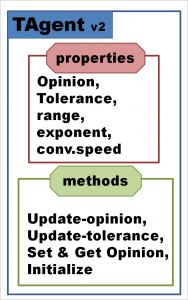
From these, it is clear that tolerance d is a property of our TAgentClass, and should as such be added. All other variables are the same for all agents in the simulation, but will change for different simulations (with the possible exception of µ). So these variable can either be defined as global variables, which conflicts with our goal of OOP, or as properties of our TAgentClass. The later also allows us to modify our TAgentClass, allowing for all agents to have different personal values for these parameters. Another added bonus is the fact that these variables do not need to be given to functions that update the opinion. Now that we have this “large” set of properties we need to think of their initialization as well. Furthermore, since the tolerance d depends on the agent’s opinion, this also means that it needs to be updated each time the opinion of the agent changes. Our new improved TAgentClass looks as follows:
- type, public :: TAgentClass
- private
- real :: oi !< opinion
- real :: di !< tolerance
- real :: mu !< global convergence speed [0-->0.5]
- real :: dmin !< min tolerance
- real :: dmax !< min tolerance
- integer :: L !< exponent for tolerance update
- contains
- private
- procedure,pass(this), public :: initialize
- procedure,pass(this), public :: getOpinion
- procedure,pass(this), public :: setOpinion
- procedure,pass(this), public :: updateOpinion
- procedure,pass(this), public :: updateTolerance
- end type TAgentClass
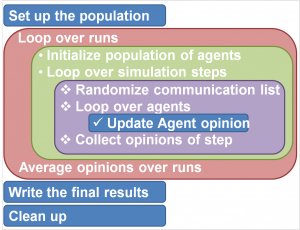
With our TAgentClass defined (and all procedures filled out), we can now setup the actual simulation and run it. This is done in the RunTutorial1 subroutine of the previous session. The first thing to do is to set up our population of agents. Generally one uses an array for such a purpose.
Following the paper, we discover that the layout of an actual simulation is a set of nested loops. There exist two levels of time-steps. The smallest one represent a single communication between two agents. We also learn that all communications are sequential and random, which means that on average each agent has two communications, one as a listener, and one as a talker. Because of this sequential nature, there is no need to have a temporary array with the previous opinion status of each agent, since it is assumed that on a second communication event the agent will be acting with his updated opinion. This is quite different from a mean field type approach where all communication happens at the same instant.
The second, larger level of time-step defines a full simulation step. In this all agents have had their two communications.
These time-steps define the two inner loops of our simulation. In addition, there is a third outer loop. Because of the random nature of the communications, the same simulation is run multiple times, and the evolution of the opinions over time (i.e. the large time-steps) is averaged over these runs. When all this is finished, we just need to write down the results, and clean up the memory (e.g. deallocate the allocatable arrays with all our agents).
Where will we be calling our TAgentClass objects?
1. During the initialization:
call agents(nr)%initialize(0.0001,0.25,1,0.25)
In this, agents is an array of TAgentClass objects, and since initialize is a subroutine it needs to be called. Because our agents are objects, we can now reach the subroutine initialize as a “part” of the TAgentClass object. In contrast, in Fortran 95 OOP one would make the call like this:
call initialize(agents(nr),0.0001,0.25,1,0.25)
2. During the opinion update:
call agents(nr)%updateOpinion(agents(talkIndex))
Again, since we are using a subroutine we use a call. Note that in both cases we do not specify in the subroutine argument list the agent that is being modified, this is being done internally through our “pass(this)” declaration in the TAgentClass declaration.
3. During data collection:
opiniondynamics(int(agents(nr)%getOpinion()*mesh)+1,nrstep)= & & opiniondynamics(int(agents(nr)%getOpinion()*mesh)+1,nrstep)+1
This command is part of a loop that just makes a histogram, and uses the agent’s opinion to find the relevant bin in our histogram. Since getOpinion is a function, we can use it as such, however, in contrast to a normal function, it now needs to be called as part of our TAgentClass-object.
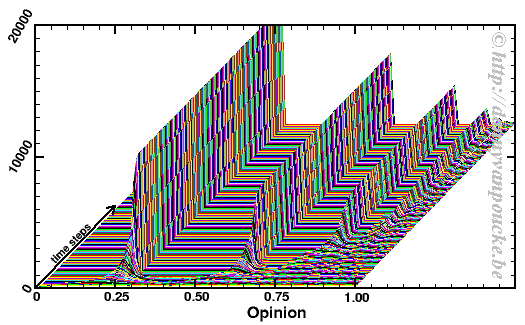
With this in hand, we now have a fully working agents program, which can run a simulation of 20K agents over 500 time steps in about 13 seconds on a 1GHz intel atom CPU (or 40-45 minutes for a 200 run full simulation, as presented in the paper). With 20 million opinion updates per run, this is already entering the realm of number-crunching or scientific computing.