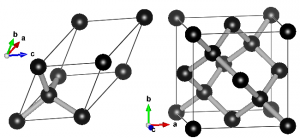
Ball-and-stick representation of diamond in two different unit cells. Left: primitive unit cell containing two atoms. All atoms at the vertices are periodic copies of the same one. Right: Conventional cubic unit cell containing eight atoms. Atoms at opposing faces are periodic copies, while all atoms at the vertices are periodic copies of the same atom.
When performing electronic structure calculations on complex systems, you prefer to do this on systems with as few atoms as possible. Such periodic cells are called unit cells. There are, however, two types of unit cells: Primitive unit cells and conventional unit cells.
A primitive unit cell is the smallest possible periodic cell of a crystalline material, making it extremely suited for calculations. Unfortunately, it is not always the nicest unit cell to work with, as it may be difficult to recognize it’s symmetry (cf. the example of diamond on the right). The conventional unit cell on the other hand shows the symmetry more clearly, but is not (always) the smallest possible unit cell. To make matters complicated and confusing, people often refer to both types as simply “unit cell”, which is not wrong, but the term unit cell is for many uniquely associated with only one of the two types.
When you are performing calculations on diamond, the conventional cell isn’t that large that standard calculations become impossible, even on a personal laptop or desktop. On the other hand, when you are studying a Metal-Organic Framework like the UiO-66(Zr) which contains 456 atoms in its conventional unit cell, you will be very happy to use the primitive unit cell with ‘merely’ 114 atoms. Also the MIL-47/53 topology which generally is studied using a conventional unit cell containing 72/76 can be reduced to a smaller primitive unit cell of only 36/38 atoms. Just as for the diamond primitive unit cell, this MIL47/53 primitive unit cell is not a nice cubic cell. Instead you end up with a lattice having lattice angles of seventy-something degrees.
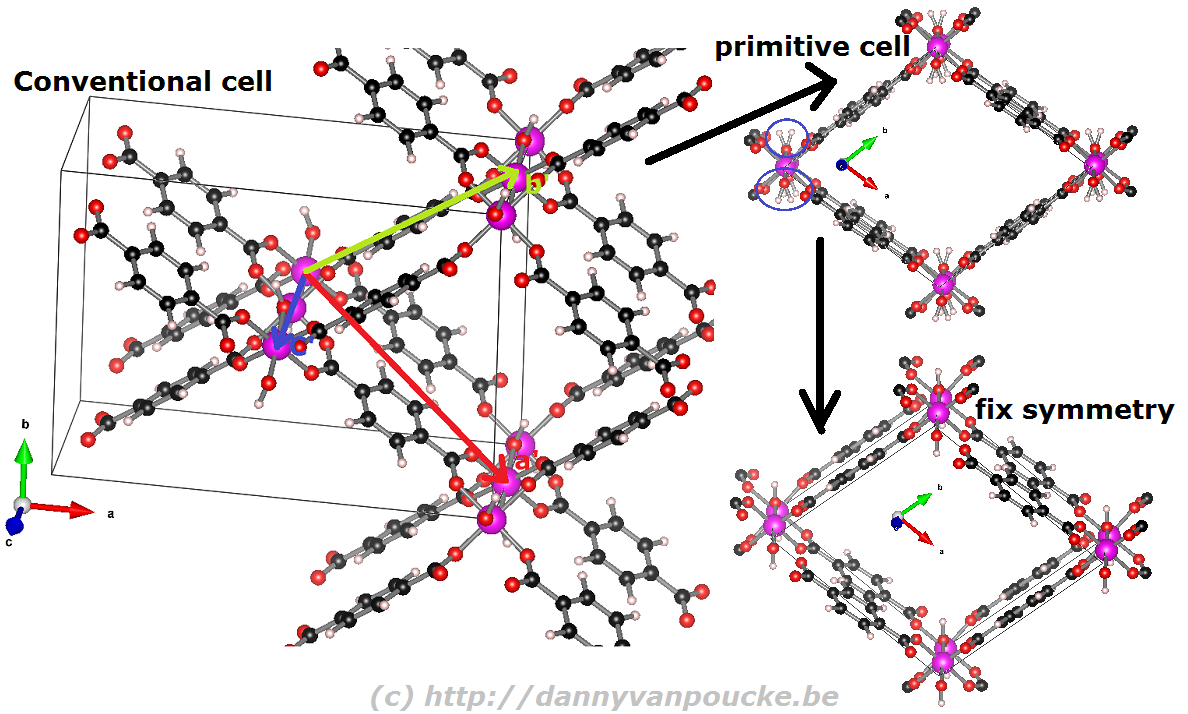
Reduction of the MIL-53 conventional cell to the primitive cell. The conventional cell is shown, extending slightly into the periodic copies. The primitive lattice vectors are shown as colored arrows. The folded primitive cell shows there was some symmetry-breaking in the hydroxy groups of the metal-oxide chain. Introducing some additional symmetry fixes this in the final primitive cell.
How to reduce a conventional unit cell to a primitive unit cell?
Before you start, and if you are using VASP, make sure you have the POSCAR file giving the atomic positions as Cartesian coordinates. (Using the HIVE-4 toolbox: Option TF, suboption 2 (Dir->Cart).)
If you do not use VASP, you can still make use of the scheme below.
- Open your structure using VESTA, and save it as “VASP” file: POSCAR.vasp (File → Export Data → choose “VASP” as filetype, select Cartesian Coordinates (don’t select the Convert to Niggli reduced cell as this only works for perfect crystal symmetry)).
- Open the file you just saved in a text editor (e.g. notepad or notepad++). The file format is quite straight forward. The first line is a comment line while the second is a general scale-factor, which for our current purpose can be ignored. What is important to know is that the 3rd, 4th and 5th lines give the lattice vectors (a, b, and c). The 6th and 7th line give the order, type and number of atoms for each atomic species (In VASP 5.x, the older VASP 4.x format does not have a 6th line). The 8th line should say “Cartesian”. From the 9th line onward you get the atomic coordinates.
- Choose 1 atom in your conventional cell which you are going to use as reference point.
- Get the primitive unit cell lattice vectors by generating vectors from the reference atom. (cf. figure above) Using VESTA this can be done as follows:
- Open your conventional cell in VESTA (if you closed it after step 1).
- Use the distance selector (5th symbol from the top in the left-hand-side menu) and for each of the primitive lattice vectors, select the reference atom and it’s primitive copy.
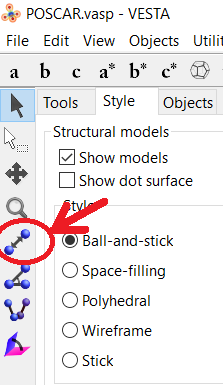
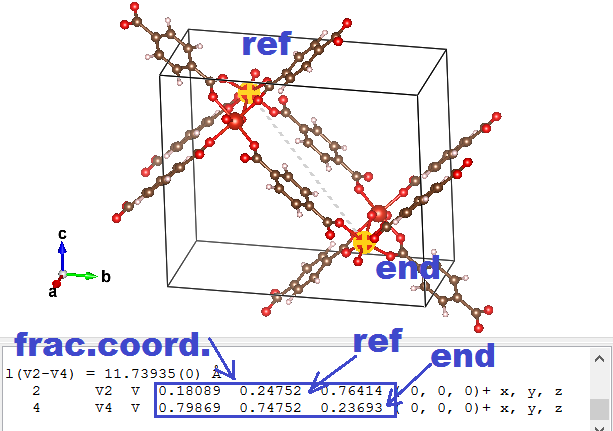
- Subtract the “fractional coordinates” of the selected atoms provided by VESTA to get a “fractional” primitive vector (the primitive a vector will be called aprim,frac )
- Multiply each of the conventional lattice vectors(aconv, bconv, and cconv) with the corresponding component of the fractional primitive vector, and add the resulting vectors to obtain the new primitive vector:
⇒ aprim = axprim,frac aconv + ayprim,frac bconv + azprim,frac cconv
So imagine that the lattice vectors of the MOF above are a = ( 20, 0, 0), b = ( 0, 15, 0), and c = ( 0, 0, 5). And the primitive fractional a vector is found to be aprim,frac = ( 0.5, -0.5, 0.5). In this case the aprim vector will become: aprim = ( 10, 0, 0 ) + ( 0, -7.5, 0 ) + ( 0, 0, 2.5) = (10, -7.5, 2.5).
- Replace the conventional lattice vectors in the POSCAR.vasp file (cf. step 2) with the new primitive lattice vectors. Save the file.
- Open the POSCAR.vasp in VESTA. If everything went well, and the conventional cell wasn’t the real primitive cell already, you should see a nice new primitive cell with the equivalent atoms perfectly overlapping one-another. This is also the reason to have your starting geometry in Cartesian coordinates. If you would have your atomic positions as fractional coordinates this first check will not work at all. Furthermore, you would need to calculate the new fractional coordinates of the atoms in the primitive unit cell. If all is well, you can close POSCAR.VASP in VESTA. (If something is wrong: either you did something wrong, and you should start again, or it wasn’t actually a super cell of a primitive cell you started to construct.)
- Get the atoms of the primitive unit cell.
- Because our atomic positions are in Cartesian coordinates in our initial geometry file, we now just need to make a list of single copies of equivalent atoms. Using VESTA (the original structure file you still have open from step 1) you can click on each atom you wish to keep and write down their index (this is the first number you find on the line with Cartesian coordinates) … For example: In case of the MIL53-MOF you can select all metal and oxygen atoms of 1 chain, and two linker molecules.
- Remove all superfluous atoms (i.e. those of which you didn’t write down the index) from the POSCAR.vasp (using your text-editor). You may want to make a backup of this file before you start :-).
- Update the number of atoms on the 7th line of the POSCAR.vasp file, and check that the number is correct. The conventional cell should have had an integer multiple of the number of atoms in the primitive cell. Save the final structure as POSCAR_final.vasp .
- The POSCAR_final.vasp should contain both the new lattice vectors and a list of atoms for a single primitive unit cell. Check this by opening the file using VESTA, and make sure you didn’t remove too many or too few atoms. If not, go back to step (a) and double check. (If you are using the HIVE4-toolbox you can first transform POSCAR_final.vasp back to direct coordinates as this may make atoms visible which nicely overlap in Cartesian coordinates: Option TF, suboption 1 (Cart->Dir) )
- Congratulations you have constructed a primitive cell from a conventional cell.
As you can see, the method is quite simple and straight forward, albeit a bit tedious if you need to do this many times.
Enjoy your primitive unit cell!
PS: Small remark for those new to VESTA. You can use delete atoms in VESTA and store your structure again. This is useful if you want to play with a molecule. Unfortunately for a solid you need also to get new lattice vectors, which did not happen. As a result you end up with some atoms floating around in a periodically repeated box with the original lattice parameters. Steps 1-5 given above provide a simple way of not ending up in this situation, but require some typing on your part.
PS 2: The opposite transformation, from a primitive unit cell to a conventional unit cell, using VESTA, is shown in this youtube video.
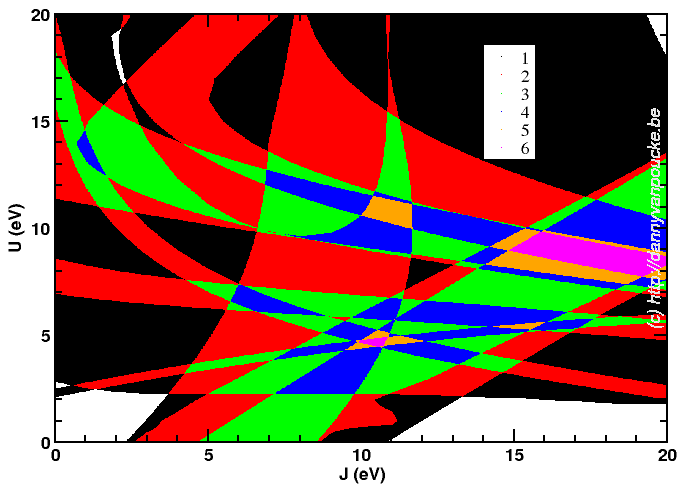

 About a year ago, I discussed the possibility of
About a year ago, I discussed the possibility of 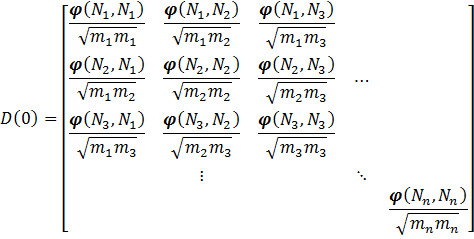
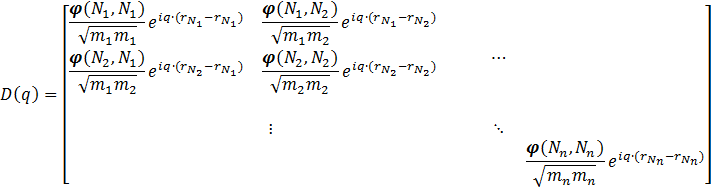
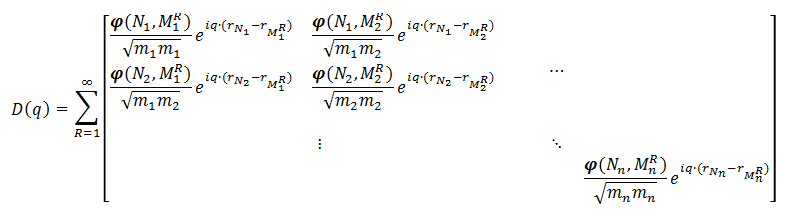
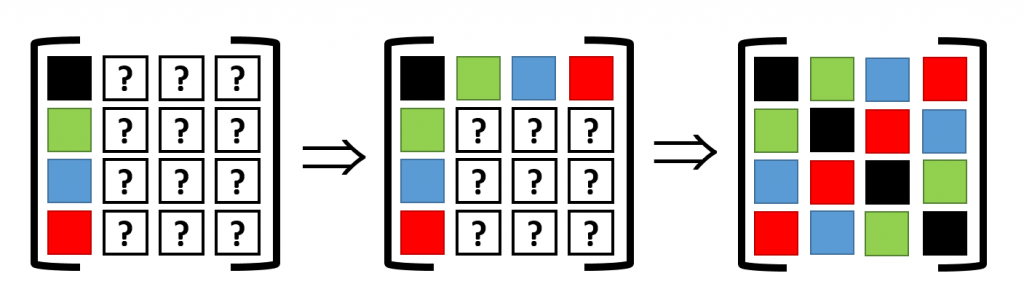
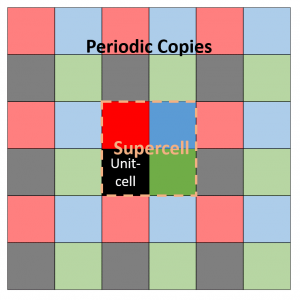 Assume a 2D 2×2 supercell with only a single atom present, which we represent as in the figure on the right. A single periodic copy of the supercell is added in each direction. The dynamical matrix for the supercell can now be constructed as follows: Calculate the elements of the first column (i.e. the gradient of the force felt by the atom in the reference unit-cell, in black, due to the atoms in each of the unit-cells in the supercell). Due to
Assume a 2D 2×2 supercell with only a single atom present, which we represent as in the figure on the right. A single periodic copy of the supercell is added in each direction. The dynamical matrix for the supercell can now be constructed as follows: Calculate the elements of the first column (i.e. the gradient of the force felt by the atom in the reference unit-cell, in black, due to the atoms in each of the unit-cells in the supercell). Due to