 About a year ago, I discussed the possibility of calculating phonons (the collective vibration of atoms) in the entire Brillouin zone for Metal-Organic Frameworks. Now, one year later, I return to this topic, but this time the subject matter is diamond. In contrast to Metal-Organic Frameworks, the unit-cell of diamond is very small (only 2 atoms). Because a phonon spectrum is calculated through the gradients of forces felt by one atom due to all other atoms, it is clear that within one diamond unit-cell these forces will not be converged. As such, a supercell will be needed to make sure the contribution, due to the most distant atoms, to the experienced forces, are negligible.
About a year ago, I discussed the possibility of calculating phonons (the collective vibration of atoms) in the entire Brillouin zone for Metal-Organic Frameworks. Now, one year later, I return to this topic, but this time the subject matter is diamond. In contrast to Metal-Organic Frameworks, the unit-cell of diamond is very small (only 2 atoms). Because a phonon spectrum is calculated through the gradients of forces felt by one atom due to all other atoms, it is clear that within one diamond unit-cell these forces will not be converged. As such, a supercell will be needed to make sure the contribution, due to the most distant atoms, to the experienced forces, are negligible.
Using such a supercell has the unfortunate drawback that the dynamical matrix (which is  , for N atoms) explodes in size, and, more importantly, that the number of eigenvalues, or phonon-frequencies also increases (
, for N atoms) explodes in size, and, more importantly, that the number of eigenvalues, or phonon-frequencies also increases (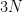 ) where we only want to have 6 frequencies (
) where we only want to have 6 frequencies ( 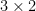 atoms) for diamond. For an
atoms) for diamond. For an  supercell we end up with
supercell we end up with  additional phonon bands which are the result of band-folding. Or put differently,
additional phonon bands which are the result of band-folding. Or put differently,  phonon bands coming from the other unit-cells in the supercell. This is not a problem when calculating the phonon density of states. It is, however, a problem when one is interested in the phonon band structure.
phonon bands coming from the other unit-cells in the supercell. This is not a problem when calculating the phonon density of states. It is, however, a problem when one is interested in the phonon band structure.
The phonon spectrum at a specific q-point in the first Brillouin zone is given by the square root of the eigenvalues of the dynamical matrix of the system. For simplicity, we first assume a finite system of n atoms (a molecule). In that case, the first Brillouin zone is reduced to a single point q=(0,0,0) and the dynamical matrix looks more or less like the hessian:
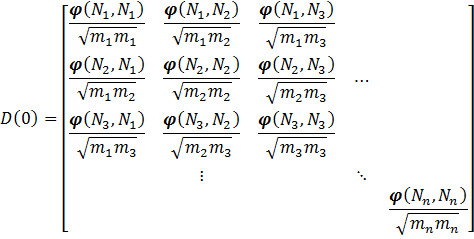
With ![\varphi (N_a,N_b) = [\varphi_{i,j}(N_a , N_b)] \varphi (N_a,N_b) = [\varphi_{i,j}(N_a , N_b)]](https://s0.wp.com/latex.php?latex=%5Cvarphi+%28N_a%2CN_b%29+%3D+%5B%5Cvarphi_%7Bi%2Cj%7D%28N_a+%2C+N_b%29%5D+&bg=ffffff&fg=000000&s=0)
 matrices
matrices  with i, j = x, y, z. Or in words,
with i, j = x, y, z. Or in words, 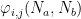 represents the derivative of the force felt by atom
represents the derivative of the force felt by atom  due to the displacement of atom
due to the displacement of atom  . Due to Newton’s second law, the dynamical matrix is expected to be symmetric.
. Due to Newton’s second law, the dynamical matrix is expected to be symmetric.
When the system under study is no longer a molecule or a finite cluster, but an infinite solid, things get a bit more complicated. For such a solid, we only consider the symmetry in-equivalent atoms (in practice this is often a unit-cell). Because the first Brillouin zone is no longer a single point, one needs to sample multiple different points to get the phonon density-of-states. The role of the q-point is introduced in the dynamical matrix through a factor  , creating a dynamical matrix for a single unit-cell containing n atoms:
, creating a dynamical matrix for a single unit-cell containing n atoms:
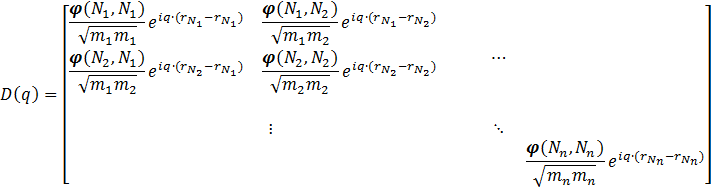
Because a real solid contains more than a single unit-cell, one should also take into account the interactions of the atoms of one unit-cell with those of all other unit-cells in the system, and as such the dynamical matrix becomes a sum of matrices like the one above:
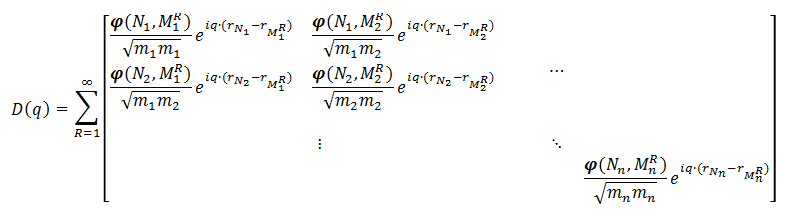
Where the sum runs over all unit-cells in the system, and Ni indicates an atom in a specific reference unit-cell, and MRi an atom in the Rth unit-cells, for which we give index 1 to the reference unit-cell. As the forces decay with the distance between the atoms, the infinite sum can be truncated. For a Metal-Organic Framework a unit-cell will quite often suffice. For diamond, however, a larger cell is needed.
An interesting aspect to the dynamical matrix above is that all matrix-elements for a sum over n unit-cells are also present in a single dynamical matrix for a supercell containing these n unit-cells. It becomes even more interesting if one notices that due to translational symmetry one does not need to calculate all elements of the entire supercell dynamical matrix to construct the full supercell dynamical matrix.
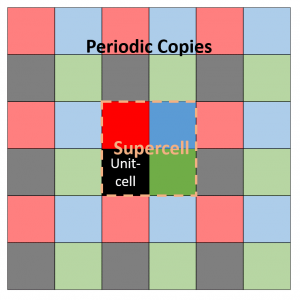 Assume a 2D 2×2 supercell with only a single atom present, which we represent as in the figure on the right. A single periodic copy of the supercell is added in each direction. The dynamical matrix for the supercell can now be constructed as follows: Calculate the elements of the first column (i.e. the gradient of the force felt by the atom in the reference unit-cell, in black, due to the atoms in each of the unit-cells in the supercell). Due to Newton’s third law (action = reaction), this first column and row will have the same elements (middle panel).
Assume a 2D 2×2 supercell with only a single atom present, which we represent as in the figure on the right. A single periodic copy of the supercell is added in each direction. The dynamical matrix for the supercell can now be constructed as follows: Calculate the elements of the first column (i.e. the gradient of the force felt by the atom in the reference unit-cell, in black, due to the atoms in each of the unit-cells in the supercell). Due to Newton’s third law (action = reaction), this first column and row will have the same elements (middle panel).
Translational symmetry on the other hand will allow us to determine all other elements. The most simple are the diagonal elements, which represent the self-interaction (so all are black squares). The other you can just as easily determine by looking at the schematic representation of the supercell under periodic boundary conditions. For example, to find the derivative of the force on the second cell (=second column, green square in supercell) due to the third cell (third row, blue square in supercell), we look at the square in the same relative position of the blue square to the green square, when starting from the black square: which is the red square (If you read this a couple of times it will start to make sense). Like this, the dynamical matrix of the entire supercell can be constructed.
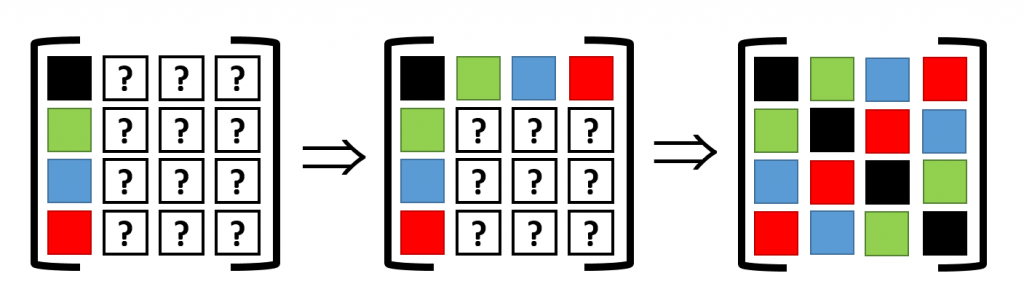
This final supercell dynamical matrix can, with the same ease, be folded back into the sum of unit-cell dynamical matrices (it becomes an extended lookup-table). The resulting unit-cell dynamical matrix can then be used to create a band structure, which in my case was nicely converged for a 4x4x4 supercell. The bandstructure along high symmetry lines is shown below, but remember that these are actually 3D surfaces. A nice video of the evolution of the first acoustic band (i.e. lowest band) as function of its energy can be found here.
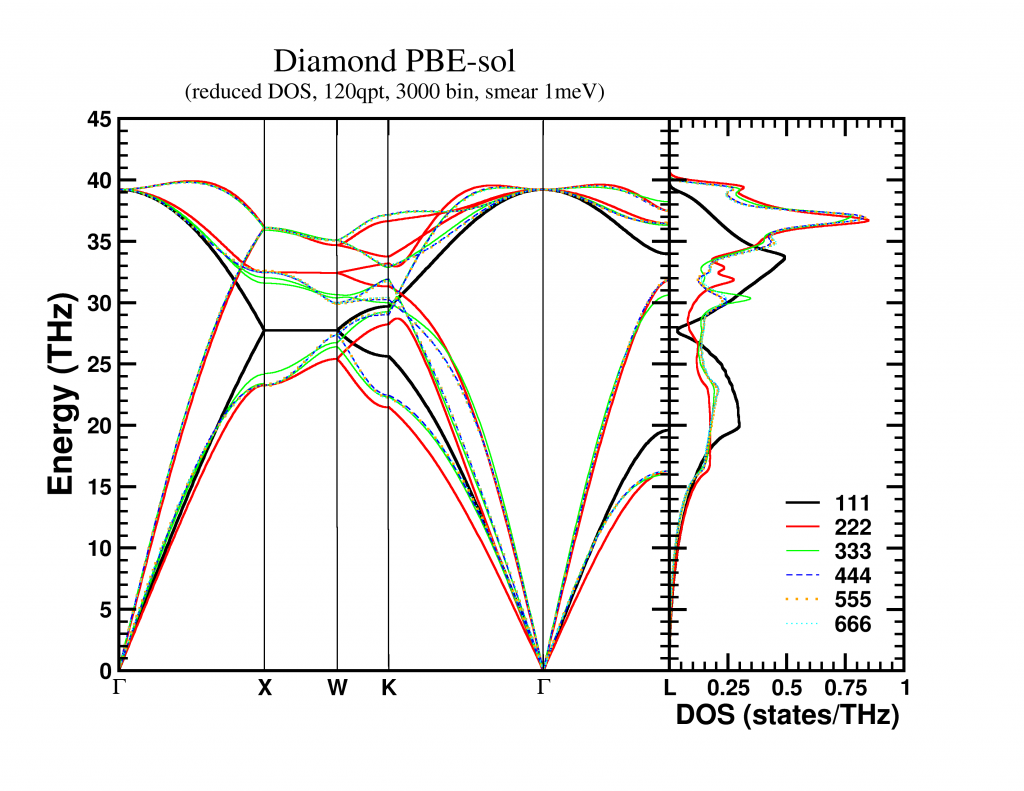
The phonon density of states can also be obtained in two ways, which should, in contrast to the band structure, give the exact same result: (for an  supercell with n atoms per unit-cell)
supercell with n atoms per unit-cell)
- Generate the density of states for the supercell and corresponding Brillouin zone. This has the advantage that the smaller Brillouin zone can be sampled with fewer q-points, as each q-point acts as M3 q-points in a unit-cell-approach. The drawback here is the fact that for each q-point a (3nM3)x(3nM3) dynamical matrix needs to be solved. This solution scales approximately as O(N3) ~ (3nM3)3 =(3n)3M9. Using linear algebra packages such as LAPACK, this may be done slightly more efficient (but you will not get O(N2) for example).
- Generate the density of states for the unit-cell and corresponding Brillouin zone. In this approach, the dynamical matrix to solve is more complex to construct (due to the sum which needs to be taken) but much smaller: 3nx3n. However to get the same q-point density, you will need to calculate M3 times as many q-points as for the supercell.
In the end, the choice will be based on whether you are limited by the accessible memory (when running a 32-bit application, the number of q-point will be detrimental) or CPU-time (solving the dynamical matrix quickly becomes very expensive).





 About a year ago, I discussed the possibility of
About a year ago, I discussed the possibility of 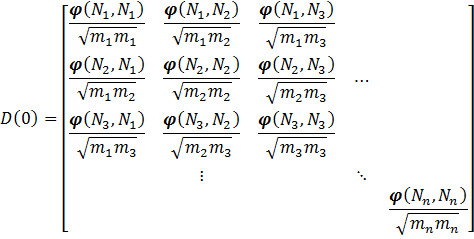
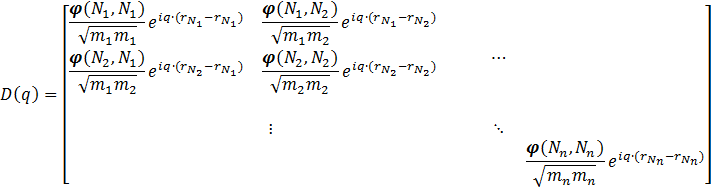
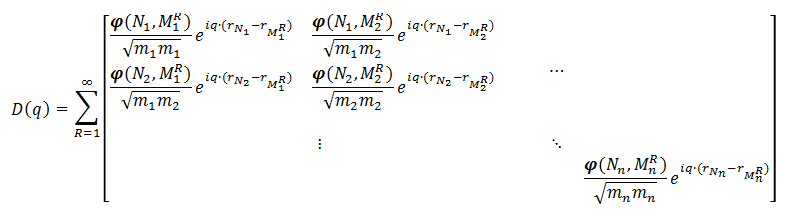
 Assume a 2D 2×2 supercell with only a single atom present, which we represent as in the figure on the right. A single periodic copy of the supercell is added in each direction. The dynamical matrix for the supercell can now be constructed as follows: Calculate the elements of the first column (i.e. the gradient of the force felt by the atom in the reference unit-cell, in black, due to the atoms in each of the unit-cells in the supercell). Due to
Assume a 2D 2×2 supercell with only a single atom present, which we represent as in the figure on the right. A single periodic copy of the supercell is added in each direction. The dynamical matrix for the supercell can now be constructed as follows: Calculate the elements of the first column (i.e. the gradient of the force felt by the atom in the reference unit-cell, in black, due to the atoms in each of the unit-cells in the supercell). Due to 

 Today was the first day of the
Today was the first day of the